如图,△ABC三个顶点坐标分别为A (1,2),B (3,1),C (2,3),以原点O为位似中心,将△ABC放大为原来的2倍得△A′B′C′.

(1)在图中第一象限内画出符合要求的△A′B′C′;(不要求写画法)
(2)△A′B′C′的面积是: .
(本小题满分7分)
(1)如图,在一次龙卷风中,一棵大树在离地面若干米处折断倒下,B为折断处最高点,树顶A落在离树根C的12米处,测得∠BAC=300,求BC的长。(结果保留根号)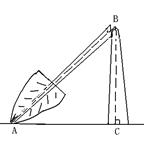
(2)如图,已知平行四边形ABCD中,点 为
为 边的中点,延长
边的中点,延长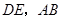 相交于点
相交于点 .
.
求证: .
.
计算: (本小题满分7分)
(1)(1)计算: .
.
(2)先化简再计算: ,其中
,其中 =3,
=3, =2.
=2.
如图,一次函数y1=k1x+2与反比例函数y2= 的图象交于点A (4,m)和B(-8,-2),与y轴交于点C
的图象交于点A (4,m)和B(-8,-2),与y轴交于点C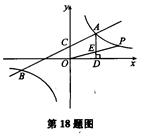
k1=_______,k2=______
根据函数图象可知,当y1>y2时,x的取值范围是______.
过点A作AD⊥x轴于点D,点P是反比例函数在第一象限的图象上一点.设直线OP与线段AD交于点E,当S四边形ODAC:S△CE=3:1时,求点P的坐标
如图,在平面直角坐标系xOy中,一次函数y=-2x的图象与反比例函数y= 的图象的一个交点为A(-1,n)
的图象的一个交点为A(-1,n)
求反比例函数y=
 的解析式
的解析式若P是坐标轴上一点,且满足PA=OA,直接写出点P的坐标.
如图,在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象与反比例函数y=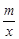 (m≠0)的图象交于第二、四象限内的A、B两点,与x轴交于C点,点B的坐标为(6,n).线段OA=5,E为x轴上一点,且sin ∠AOE=
(m≠0)的图象交于第二、四象限内的A、B两点,与x轴交于C点,点B的坐标为(6,n).线段OA=5,E为x轴上一点,且sin ∠AOE=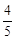 .
.
求该反比例函数和一次函数的解析式
求△AOC的面积