(本小题满分14分)已知关于 的函数
的函数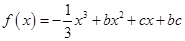 ,其导函数为
,其导函数为 .记函数
.记函数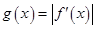 在区间
在区间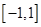 上的最大值为
上的最大值为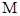 .
.
(1)如果函数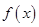 在
在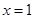 处有极值
处有极值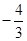 ,试确定
,试确定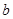 、
、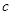 的值;
的值;
(2)若 ,证明:对任意的
,证明:对任意的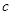 ,都有
,都有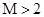 ;
;
(3)若 对任意的
对任意的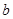 、
、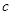 恒成立,试求
恒成立,试求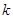 的最大值.
的最大值.
(本小题满分12分)
为应对金融危机,刺激消费,某市给市民发放旅游消费卷,由抽样调查预计老、中、青三类市民持有这种消费卷到某旅游景点消费额及其概率如下表:
  |
200元 |
300元 |
400元 |
500元 |
| 老年 |
0.4 |
0.3 |
0.2 |
0.1 |
| 中年 |
0.3 |
0.4 |
0.2 |
0.1 |
| 青年 |
0.3 |
0.3 |
0.2 |
0.2 |
某天恰好有持有这种消费卷的老年人、中年人、青年人各一人到该旅游景点,
(Ⅰ)求这三人消费总额大于1300元的概率;
(Ⅱ)设这三人中消费额大于300元的人数为 ,求
,求 的分布列及数学期望。
的分布列及数学期望。
(本小题满分12分)
如图, 在直三棱柱ABC-A1B1C1中,AC=3 ,BC=4,
,BC=4, ,AA1=4,点D是AB的中点.
,AA1=4,点D是AB的中点.
(Ⅰ)求证:AC⊥BC1;
(Ⅱ)求二面角 的余弦值.
的余弦值.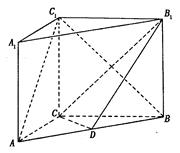
(本小题满分14分)
设函数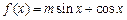
 的图象经过点
的图象经过点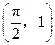 .
.
(Ⅰ)求 的解析式,并求函数的最小正周期和最值.
的解析式,并求函数的最小正周期和最值.
(Ⅱ)若 ,其中
,其中 是面积为
是面积为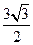 的锐角
的锐角 的内角,且
的内角,且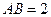 ,
,
求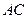 和
和 的长.
的长.
已知函数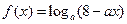
(1)若 ,求实数
,求实数 的取值范围;
的取值范围;
(2)若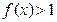 在区间[1,2]上恒成立,求实数
在区间[1,2]上恒成立,求实数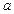 的取值范围.
的取值范围.
若数列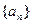 的前
的前 项和为
项和为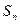 ,点
,点 均在函数
均在函数 的图象上
的图象上
(1)求数列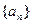 的通项公式;
的通项公式;
(2)若数列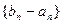 是首项为1,公比为
是首项为1,公比为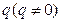 的等比数列,求数列
的等比数列,求数列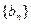 的前
的前 项和
项和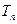 .
.