(本题满分12分)已知函数 .
.
(1)证明: ;
;
(2)当 时,
时, 恒成立,求
恒成立,求 的取值范围.
的取值范围.
为了研究玉米品种对产量的影响,某农科院对一块试验田种植的一批玉米共10000株的生长情况进行研究,现采用分层抽样方法抽取50株作为样本,统计结果如下:
| 高茎 |
矮茎 |
合计 |
|
| 圆粒 |
11 |
19 |
30 |
| 皱粒 |
13 |
7 |
20 |
| 合计 |
24 |
26 |
50 |
(1) 现采用分层抽样的方法,从这个样本中取出10株玉米,再从这10株玉米中随机选出3株,求选到的3株之中既有圆粒玉米又有皱粒玉米的概率;
(2) 根据对玉米生长情况作出的统计,是否能在犯错误的概率不超过0.050的前提下认为玉米的圆粒与玉米的高茎有关?(下面的临界值表和公式可供参考:
| P(K2≥k) |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
| k |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
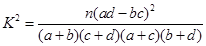 ,其中
,其中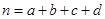 )
)
数列 满足
满足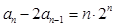
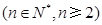 ,且
,且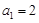 .
.
(1) 求数列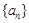 的通项公式;
的通项公式;
(2) 令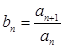 ,当数列
,当数列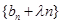 为递增数列时,求正实数
为递增数列时,求正实数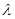 的取值范围.
的取值范围.
在平面直角坐标系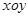 中,已知椭圆
中,已知椭圆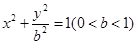 的左焦点为
的左焦点为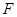 ,左、右顶点分别为
,左、右顶点分别为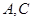 ,上顶点为
,上顶点为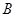 ,过
,过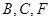 三点作圆
三点作圆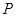
(Ⅰ)若线段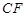 是圆
是圆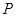 的直径,求椭圆的离心率;
的直径,求椭圆的离心率;
(Ⅱ)若圆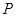 的圆心在直线
的圆心在直线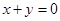 上,求椭圆的方程;
上,求椭圆的方程;
(Ⅲ)若直线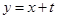 交(Ⅱ)中椭圆于
交(Ⅱ)中椭圆于 ,交
,交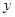 轴于
轴于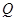 ,求
,求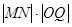 的最大值
的最大值
已知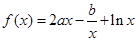 在
在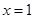 与
与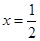 处都取得极值.
处都取得极值.
(Ⅰ) 求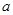 ,
,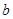 的值;
的值;
(Ⅱ)设函数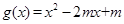 ,若对任意的
,若对任意的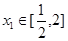 ,总存在
,总存在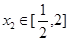 ,使得、
,使得、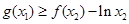 ,求实数
,求实数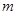 的取值范围.
的取值范围.
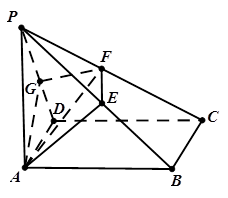
如图所示,四棱锥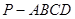 ,底面
,底面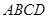 是边长为
是边长为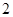 的正方形,
的正方形,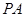 ⊥面
⊥面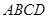 ,
,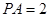 ,过点
,过点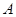 作
作 ,连接
,连接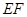 .
.
(Ⅰ)求证: ;
;
(Ⅱ)若面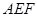 交侧棱
交侧棱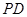 于点
于点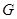 ,求多面体
,求多面体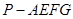 的体积.
的体积.