(本小题满分10分)选修4-4:坐标系与参数方程
已知曲线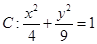 ,直线
,直线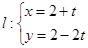 (
(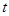 为参数)
为参数)
写出曲线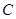 的参数方程,直线
的参数方程,直线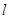 的普通方程;
的普通方程;
过曲线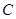 上任意一点
上任意一点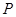 作与
作与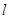 夹角为30°的直线,交
夹角为30°的直线,交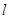 于点
于点 ,求
,求 的最大值与最小值.
的最大值与最小值.
二十世纪50年代,日本熊本县水俣市的许多居民都患了运动失调、四肢麻木等症状,人们把它称为水俣病.经调查发现一家工厂排出的废水中含有甲基汞,使鱼类受到污染.人们长期食用含高浓度甲基汞的鱼类引起汞中毒. 引起世人对食品安全的关注.《中华人民共和国环境保护法》规定食品的汞含量不得超过1.00ppm.
罗非鱼是体型较大,生命周期长的食肉鱼,其体内汞含量比其他鱼偏高.现从一批罗非鱼中随机地抽出15条作样本,经检测得各条鱼的汞含量的茎叶图(以小数点前一位数字为茎,小数点后一位数字为叶)如下:
(Ⅰ)若某检查人员从这15条鱼中,随机地抽出3条,求恰有1条鱼汞含量超标的概率;
(Ⅱ)以此15条鱼的样本数据来估计这批鱼的总体数据.若从这批数量很大的鱼中任选3条鱼,记ξ表示抽到的鱼汞含量超标的条数,求ξ的分布列及Eξ
图1,平面四边形 关于直线
关于直线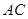 对称,
对称,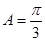 ,
,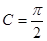 ,
, .把
.把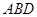 沿
沿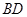 折起(如图2),使二面角
折起(如图2),使二面角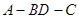 的余弦值等于
的余弦值等于 .
.
对于图二,完成以下各小题:
(Ⅰ)求 两点间的距离;
两点间的距离;
(Ⅱ)证明: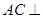 平面
平面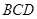 ;
;
(Ⅲ)求直线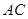 与平面
与平面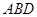 所成角的正弦值.
所成角的正弦值.
已知向量
(Ⅰ)求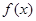 的解析式;
的解析式;
(Ⅱ)求由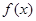 的图象、
的图象、 轴的正半轴及
轴的正半轴及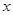 轴的正半轴三者围成图形的面积。
轴的正半轴三者围成图形的面积。
在等差数列 中,
中,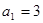 ,其前
,其前 项和为
项和为 ,等比数列
,等比数列 的各项均为正数,
的各项均为正数, ,公比为
,公比为 ,且
,且 ,
, 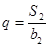 .
.
(Ⅰ)求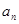 与
与 ;
;
(Ⅱ)证明: .
.
(本小题满分10分)
(1)解不等式
(2)设x,y,z 且
且 ,求
,求 的最小值.
的最小值.