本小题满分13分)在四边形 中,
中, ,且
,且 ,求
,求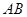 的长.
的长.
已知函数f(x)=a +bx-a-ab(a≠0),当
+bx-a-ab(a≠0),当 时,f(x)>0;当
时,f(x)>0;当 时,f(x)<0.
时,f(x)<0.
(1)求f(x)在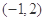 内的值域;
内的值域;
(2)若方程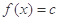 在
在 有两个不等实根,求c的取值范围.
有两个不等实根,求c的取值范围.
已知函数f(x)=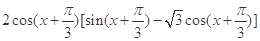 .
.
(1)求f(x)的值域和最小正周期;
(2)方程m[f(x)+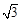 ]+2=0在
]+2=0在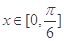 内有解,求实数m的取值范围.
内有解,求实数m的取值范围.
(本小题15分)设动点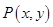
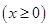 到定点
到定点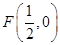 的距离比到
的距离比到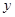 轴的距离大
轴的距离大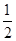 .记点
.记点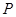 的轨迹为曲线C.
的轨迹为曲线C.
(1)求点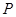 的轨迹方程;
的轨迹方程;
(2)设圆M过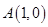 ,且圆心M在P的轨迹上,
,且圆心M在P的轨迹上,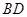 是圆M在
是圆M在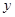 轴上截得的弦,当圆心M运动时弦长
轴上截得的弦,当圆心M运动时弦长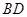 是否为定值?说明理由;
是否为定值?说明理由;
(3)过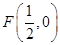 作互相垂直的两直线交曲线C于G、H、R、S,求四边形
作互相垂直的两直线交曲线C于G、H、R、S,求四边形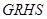 面积的最小值.
面积的最小值.
(本小题15分)已知正方形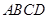 的边长为
的边长为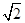 ,
,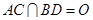 .将正方形
.将正方形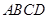 沿对角线
沿对角线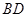 折起,使
折起,使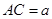 ,得到三棱锥
,得到三棱锥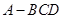 ,如图所示.
,如图所示.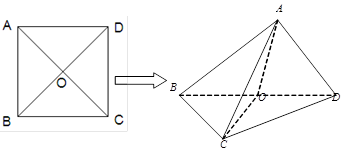
(1)当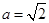 时,求证:
时,求证: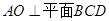 ;
;
(2)当二面角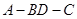 的大小为
的大小为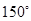 时,求AB与平面BCD所成角的正弦值.
时,求AB与平面BCD所成角的正弦值.
(本小题14分)已知函数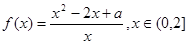 ,其中常数a > 0.
,其中常数a > 0.
(1)当a = 4时,证明函数f(x)在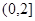 上是减函数;
上是减函数;
(2)求函数f(x)的最小值.