（本小题12分）某次的一次学科测试成绩的茎叶图和频率分布直方图都受到不同程度的污损，可见部分如图．
（Ⅰ）求参加测试的总人数及分数在[80，90）之间的人数；
（Ⅱ）若要从分数在[80，100）之间的试卷中任取两份分析学生失分情况，求在抽取的试卷中，恰有一份分数在[90，100）之间的概率．
（
某有奖销售将商品的售价提高120元后允许顾客有3次抽奖的机会，每次抽奖的方法是在已经设置并打开了程序的电脑上按“Enter”键，电脑将随机产生一个1~6的整数数作为号码，若该号码是3的倍数则顾客获奖，每次中奖的奖金为100元，运用所学的知识说明这样的活动对商家是否有利。
（
已知圆的极坐标方程为：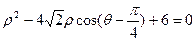
.
将极坐标方程化为普通方程，写出圆的参数方程。
若点P（x
,y）在该圆上，求x+y的最大值和最小值。
已知
，且正整数n满足
，
（1）求n ；
（2）若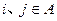
，是否存在
，当
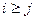时，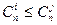
恒成立。若存在，求出最小的；
若不存在，试说明理由。
（3）
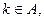若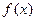
的展开式有且只有三个有理项，求
。
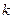已知矩阵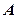
=
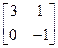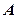，求的特征值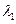
，
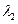及对应的特征向量
．
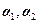（ （本小题满分14分）
已知函数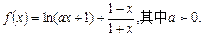
（1）求
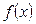在x=1处取得极值；
（2）求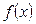的单
调区间；
（3）若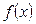的最小值为1，求a的取值范围.