(本小题满分12分)如图是某几何体的直观图与三视图的侧视图、俯视图.在直观图中,2BN=AE,M是ND的中点.侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.
(1)在答题纸上的虚线框内画出该几何体的正视图,并标上数据;
(2)求证:EM∥平面ABC;
(3)试问在边BC上是否存在点G,使GN⊥平面NED.若存在,确定点G的位置;若不存在,请说明理由.
(本题满分18分,第(1)小题4分,第(2)小题6分,第(3)小题8分)
如图所示的“8”字形曲线是由两个关于 轴对称的半圆和一个双曲线的一部分组成的图形,其中上半个圆所在圆方程是
轴对称的半圆和一个双曲线的一部分组成的图形,其中上半个圆所在圆方程是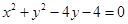 ,双曲线的左、右顶点
,双曲线的左、右顶点 、
、 是该圆与
是该圆与 轴的交点,双曲线与半圆相交于与
轴的交点,双曲线与半圆相交于与 轴平行的直径的两端点.
轴平行的直径的两端点.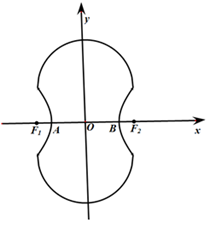
(1)试求双曲线的标准方程;
(2)记双曲线的左、右焦点为 、
、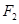 ,试在“8”字形 曲线上求点
,试在“8”字形 曲线上求点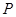 ,使得
,使得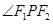 是直角.
是直角.
(3)过点 作直线
作直线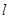 分别交“8”字形曲线中上、下两个半圆于点
分别交“8”字形曲线中上、下两个半圆于点 ,求
,求 的最大长度.
的最大长度.
(本题满分16分,第(1)小题7分,第(2)小题9分)
如图,在两块钢板上打孔,用钉帽呈半球形、钉身为圆柱形的铆钉(图1)穿在一起,在没有帽的一端锤打出一个帽,使得与钉帽的大小相等.铆合的两块钢板,成为某种钢结构的配件,其截面图如图2.(单位:mm,加工中不计损失).
(1)若钉身长度是钉帽高度的2倍,求铆钉的表面积;
(2)若每块钢板的厚度为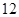 mm,求钉身的长度(结果精确到
mm,求钉身的长度(结果精确到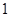 mm).
mm).
(本题满分14分,第(1)小题6分,第(2)小题8分)
如图,在四棱锥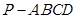 中,底面
中,底面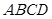 为矩形,
为矩形, 平面
平面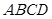 ,点
,点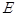 在线段
在线段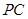 上,
上,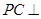 平面
平面 .
.
(1)求证: 平面
平面 ;
;
(2)若 ,
, ,求二面角
,求二面角 的大小.
的大小.
(本题满分14分,第(1)小题6分,第(2)小题8分)
如图,已知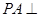 平面
平面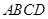 ,
, ,
,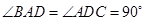 .
.
(1)求直线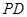 与平面
与平面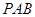 所成角的大小;
所成角的大小;
(2)求点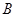 到平面
到平面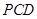 的距离.
的距离.
(本题满分12分,第(1)小题4分,第(2)小题8分)
如图,在体积为16的正四棱柱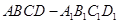 中,点
中,点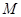 是
是 的中点,
的中点, .
.
(1)求棱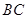 的长;
的长;
(2)求异面直线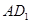 与
与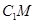 所成角的大小.
所成角的大小.