病毒虽无情,人间有大爱.2020年,在湖北省抗击新冠病毒的战"疫"中,全国(除湖北省外)共有30个省(区、市)及军队的医务人员在党中央全面部署下,白衣执甲,前赴后继支援湖北省.全国30个省(区、市)各派出支援武汉的医务人员频数分布直方图(不完整)和扇形统计图如下:(数据分成6组: , , , , , .

根据以上信息回答问题:
(1)补全频数分布直方图.
(2)求扇形统计图中派出人数大于等于100小于500所占圆心角度数.
据新华网报道,在支援湖北省的医务人员大军中,有"90后"也有"00后",他们是青春的力量,时代的脊梁.小华在收集支援湖北省抗疫宣传资料时得到这样一组有关"90后"医务人员的数据:
市派出的1614名医护人员中有404人是"90后";
市派出的338名医护人员中有103人是"90后";
市某医院派出的148名医护人员中有83人是"90后".
(3)请你根据小华得到的这些数据估计在支援湖北省的全体医务人员(按4.2万人计)中,"90后"大约有多少万人?(写出计算过程,结果精确到0.1万人)
如图,在 中, ,过 的中点 作 , ,垂足分别为点 、 .
(1)求证: ;
(2)若 ,求 的度数.
一个不透明的盒子里装有除颜色外其余均相同的2个黑球和 个白球,搅匀后从盒子里随机摸出一个球,摸到白球的概率为 .
(1)求 的值;
(2)所有球放入盒中,搅匀后随机从中摸出1个球,放回搅匀,再随机摸出第2个球,求两次摸球摸到一个白球和一个黑球的概率.请用画树状图或列表的方法进行说明.
化简: .
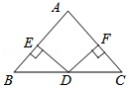
如图1,抛物线 与 轴交于 , ,与 轴交于点 .已知直线 过 , 两点.
(1)求抛物线和直线 的表达式;
(2)点 是抛物线上的一个动点.
①如图1,若点 在第一象限内,连接 ,交直线 于点 .设 的面积为 , 的面积为 ,求 的最大值;
②如图2,抛物线的对称轴 与 轴交于点 ,过点 作 ,垂足为 .点 是对称轴 上的一个动点,是否存在以点 , , , 为顶点的四边形是平行四边形?若存在,求出点 , 的坐标;若不存在,请说明理由.