甲、乙两人玩一种抽卡片游戏，将背面完全相同，正面分别写有1、-优题课

甲、乙两人玩一种抽卡片游戏，将背面完全相同，正面分别写有1、2、3、4的四张卡片背面朝上混合后，甲从中随机抽取一张，记下数字，把卡片放回后，乙再从中随机抽取一张，记下数字，如果所得两数之和大于4，则甲胜；如果所得两数之和不大于4，则乙胜。
⑴请用列表法或画树状图的方法，分别求甲、乙获胜的概率来说明游戏公平吗？
⑵按游戏规则求甲、乙各取一次卡片，取出的数字相同的概率。

科目数学题型解答题难度中等

知识点：利用频率估计概率

计算：

（1） ${(2 m + 3 n)}^{2} - (2 m + n) (2 m - n)$ ；

（2） $\frac{x - y}{x} \div (x + \frac{y^{2} - 2 xy}{x})$ ．

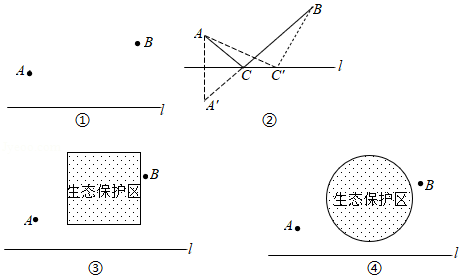
如图①，要在一条笔直的路边 $l$ 上建一个燃气站，向 $l$ 同侧的 $A$ 、 $B$ 两个城镇分别铺设管道输送燃气．试确定燃气站的位置，使铺设管道的路线最短．

（1）如图②，作出点 $A$ 关于 $l$ 的对称点 $A^{'}$ ，线段 $A^{'} B$ 与直线 $l$ 的交点 $C$ 的位置即为所求，即在点 $C$ 处建燃气站，所得路线 $ACB$ 是最短的．

为了证明点 $C$ 的位置即为所求，不妨在直线1上另外任取一点 $C^{'}$ ，连接 $A C^{'}$ 、 $B C^{'}$ ，证明 $AC + CB < AC' + C^{'} B$ ．请完成这个证明．

（2）如果在 $A$ 、 $B$ 两个城镇之间规划一个生态保护区，燃气管道不能穿过该区域．请分别给出下列两种情形的铺设管道的方案（不需说明理由）．

①生态保护区是正方形区域，位置如图③所示；

②生态保护区是圆形区域，位置如图④所示．

如图，在 $ΔABC$ 和△ $A^{'} B^{'} C^{'}$ 中， $D$ 、 $D^{'}$ 分别是 $AB$ 、 $A^{'} B^{'}$ 上一点， $\frac{AD}{AB} = \frac{A' D'}{A' B'}$ ．

（1）当 $\frac{CD}{C' D'} = \frac{AC}{A' C'} = \frac{AB}{A' B'}$ 时，求证 $ΔABC ∽$ △ $A^{'} B^{'} C^{'}$ ．

证明的途径可以用下面的框图表示，请填写其中的空格．

（2）当 $\frac{CD}{C' D'} = \frac{AC}{A' C'} = \frac{BC}{B' C'}$ 时，判断 $ΔABC$ 与△ $A^{'} B^{'} C'$ 是否相似，并说明理由．

小明和小丽先后从 $A$ 地出发沿同一直道去 $B$ 地．设小丽出发第 $xmin$ 时，小丽、小明离 $B$ 地的距离分别为 $y_{1} m$ 、 $y_{2} m$ ． $y_{1}$ 与 $x$ 之间的函数表达式是 $y_{1} = - 180 x + 2250$ ， $y_{2}$ 与 $x$ 之间的函数表达式是 $y_{2} = - 10 x^{2} - 100 x + 2000$ ．

（1）小丽出发时，小明离 $A$ 地的距离为　　 $m$ ．

（2）小丽出发至小明到达 $B$ 地这段时间内，两人何时相距最近？最近距离是多少？

如图，在 $ΔABC$ 中， $AC = BC$ ， $D$ 是 $AB$ 上一点， $⊙ O$ 经过点 $A$ 、 $C$ 、 $D$ ，交 $BC$ 于点 $E$ ，过点 $D$ 作 $DF / / BC$ ，交 $⊙ O$ 于点 $F$ ．

求证：（1）四边形 $DBCF$ 是平行四边形；

（2） $AF = EF$ ．