为了解某中学全校学生对排球、乒乓球、篮球、羽毛球、足球五项体育运动的喜爱情况,从中随机调查了若干名学生,并将调查结果绘制成统计表和统计图(不完整).
| 项目 |
人数 |
百分比 |
| 排球 |
10 |
5% |
| 乒乓球 |
45 |
|
| 篮球 |
58 |
29% |
| 羽毛球 |
|
37.5% |
| 足球 |
12 |
6% |
请根据图中提供的信息,解答下列问题:
(1)补全统计表和统计图.
(2)根据以上调查,估计该校1800名学生中,喜欢羽毛球的人数是多少?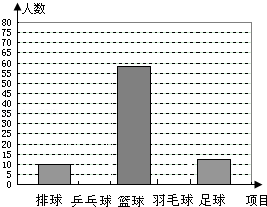
在正方形ABCD中,点E,F分别在边BC,CD上,且∠EAF=∠CEF=45°.
(1)将△ADF绕着点A顺时针旋转90°,得到△ABG(如图①),求证:△AEG≌△AEF;
(2)若直线EF与AB,AD的延长线分别交于点M,N(如图②),求证: ;
;
(3)将正方形改为长与宽不相等的矩形,若其余条件不变(如图③),请你直接写出线段EF,BE,DF之间的数量关系.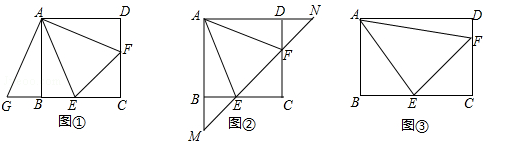
某校在基地参加社会实践话动中,带队老师考问学生:基地计划新建一个矩形的生物园地,一边靠旧墙(墙足够长),另外三边用总长69米的不锈钢栅栏围成,与墙平行的一边留一个宽为3米的出入口,如图所示,如何设计才能使园地的而积最大?下面是两位学生争议的情境:
请根据上面的信息,解决问题:
(1)设AB=x米(x>0),试用含x的代数式表示BC的长;
(2)请你判断谁的说法正确,为什么?
如图,在矩形ABCD中.点O在边AB上,∠AOC=∠BOD.求证:AO=OB.
如图,菱形ABCD的对角线AC,BD相交于点O,点E,F分别是边AB,AD的中点.
(1)请判断△OEF的形状,并证明你的结论;
(2)若AB=13,AC=10,请求出线段EF的长.
下列网格中的六边形ABCDEF是由边长为6的正方形左上角剪去边长为2的正方形所得,该六边形按一定的方法可剪拼成一个正方形.
(1)根据剪拼前后图形的面积关系求出拼成的正方形的边长;
(2)如图甲,把六边形ABCDEF沿EH,BG剪成①②③三部分,请在图甲中画出将②③与①拼成的正方形,然后标出②③变动后的位置,并指出②③属于旋转、平移和轴对称中的哪一种变换;
(3)在图乙中画出一种与图甲不同位置的两条裁剪线,并在图乙中画出将此六边形剪拼成的正方形.