甲骑自行车、乙骑摩托车沿相同路线由A地到B地,行驶过程中路程与时间的函数关系的图象如图.根据图象解决下列问题: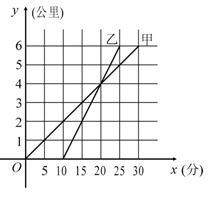
(1)谁先出发?先出发多少时间?谁先到达终点?先到多少时间?
(2)分别求出甲、乙两人的行驶速度;
(3)在什么时间段内,两人均行驶在途中(不包括起点和终点)?在这一时间段内,请你根据下列情形,分别列出关于行驶时间x的方程或不等式(不化简,也不求解):① 甲在乙的前面;② 甲与乙相遇;③ 甲在乙后面.
某超市销售樱桃,已知樱桃的进价为15元 千克,如果售价为20元 千克,那么每天可售出250千克,如果售价为25元 千克,那么每天可获利2000元,经调查发现:每天的销售量 (千克)与售价 (元 千克)之间存在一次函数关系.
(1)求 与 之间的函数关系式;
(2)若樱桃的售价不得高于28元 千克,请问售价定为多少时,该超市每天销售樱桃所获的利润最大?最大利润是多少元?
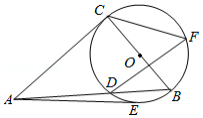
如图, 中, ,以 为直径的 交 于点 , 、 是 上两点,连接 、 、 ,满足 .
(1)求证: 是 的切线;
(2)若 的半径为3, ,求 的长.
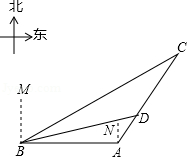
今年,我国海关总署严厉打击“洋垃圾”违法行动,坚决把“洋垃圾”拒于国门之外.如图,某天我国一艘海监船巡航到 港口正西方的 处时,发现在 的北偏东 方向,相距150海里处的 点有一可疑船只正沿 方向行驶, 点在 港口的北偏东 方向上,海监船向 港口发出指令,执法船立即从 港口沿 方向驶出,在 处成功拦截可疑船只,此时 点与 点的距离为 海里.
(1)求 点到直线 的距离;
(2)执法船从 到 航行了多少海里?(结果保留根号)
近年来雾霾天气给人们的生活带来很大影响,空气质量问题倍受人们关注.某单位计划在室内安装空气净化装置,需购进 、 两种设备.每台 种设备价格比每台 种设备价格多0.7万元,花3万元购买 种设备和花7.2万元购买 种设备的数量相同.
(1)求 种、 种设备每台各多少万元?
(2)根据单位实际情况,需购进 、 两种设备共20台,总费用不高于15万元,求 种设备至少要购买多少台?
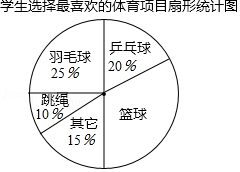
某校以“我最喜爱的体育项目”为主题对全校学生进行随机抽样调查,调查的运动项目有:篮球、羽毛球、乒乓球、跳绳及其它项目(每位同学仅选一项),根据调查数据绘制了如下不完整的统计表和扇形统计图:
学生选择最喜爱的体育项目统计表
|
运动项目 |
频数(人数) |
频率 |
|
篮球 |
36 |
0.30 |
|
羽毛球 |
|
0.25 |
|
乒乓球 |
24 |
|
|
跳绳 |
12 |
0.10 |
|
其它项目 |
18 |
0.15 |
请根据以上图表信息解答下列问题:
(1)统计表中的 , ;
(2)在扇形统计图中,“篮球”所在扇形的圆心角为 度;
(3)该学校共有2400名学生,据此估计有多少名学生最喜爱乒乓球?
(4)将2名最喜爱篮球的学生和2名最喜爱羽毛球的学生编为一组,从中随机抽取两人,请用列表或画树状图的方法求出所抽取的两人都选择了最喜爱篮球的概率.