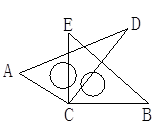已知:在△ABC中,∠ABC<60°,CD平分∠ACB交AB于点D,点E在线段CD上(点E不与点C,D重合),且∠EAC=2∠EBC.
(1)如图1,若∠EBC=27°,且EB=EC,则∠DEB= °,∠AEC= °;
(2)如图2.①求证:AE+AC=BC; ②若∠ECB=30°,且AC=BE,求∠EBC的度数.
市实验中学学生步行到郊外旅行。高一(1)班学生组成前队,步行速度为4千米/时,高一(2)班学生组成后队,速度为6千米/时。前队出发1小时后,后队才出发,同时后队派一名联络员骑自行车在两队之间不间断地来回进行联络,他骑车的速度为12千米/时。
(1)后队追上前队需要多长时间?
(2)后队追上前队时间内,联络员走的路程是多少?
(3)两队何时相距2千米?
我市某会议厅主席台上方有一个长12.8m的长条形(矩形)会议横标框,铺红色衬底.开会前将会议名称用白色厚纸或不干胶纸刻出来贴于其上.但会议名称不同,字数一般每次都多少不等,为了制作及贴字时方便美观,会议厅工作人员对有关数据作了如下规定:边空:字宽:字距=9:6:2,如图所示.
根据这个规定,求会议名称的字数为18时,边空、字宽、字距各是多少cm?
如图,点C在线段AB上,AC ="16" cm,CB ="12" cm,点M、N分别是AC、BC的中点。
(1)求线段MN的长;
(2)若C为线段AB上任一点,满足AC + CB =" a" cm,其它条件不变,你能猜想MN的长度吗?并说明理由。
(3)若C在线段AB的延长线上,且满足AC BC =" b" cm,M、N分别为AC、BC的中点,你能猜想MN的长度吗?请画出图形,写出你的结论,不要说明理由。
BC =" b" cm,M、N分别为AC、BC的中点,你能猜想MN的长度吗?请画出图形,写出你的结论,不要说明理由。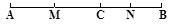
如图1,是棱长为 的小正方体,图2,图3由这样的小正方体摆放而成。按照这样的方法继续摆放,自上而下分别叫第一层、第二层、……、第
的小正方体,图2,图3由这样的小正方体摆放而成。按照这样的方法继续摆放,自上而下分别叫第一层、第二层、……、第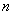 层,第
层,第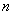 层的小正方体的个数记为s。解答下列问题:
层的小正方体的个数记为s。解答下列问题:
(1)按照要求填表:
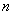 |
1 |
2 |
3 |
4 |
… |
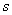 |
1 |
3 |
6 |
… |
(2)当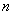 =10时,求s的值。
=10时,求s的值。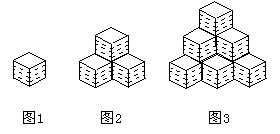
如图,将两块直角三角尺的直角顶点C叠放在一起.
(1)若∠DCE=350,求∠ACB的度数;
(2)若∠ACB=1400,求∠DCE的度数;
(3)猜想:∠ACB与∠DCE有怎样的数量关系,并说明理由.