在数列 中,已知
中,已知 ,
, ,
, ,
, ,数列
,数列 的前
的前 项和为
项和为 ,数列
,数列 的前
的前 项和为
项和为 ,且满足
,且满足 ,
, ,其中
,其中 为正整数.
为正整数.
(1)求数列 的通项公式;
的通项公式;
(2)问是否存在正整数 ,
, ,使
,使 成立?若存在,求出所有符合条件的有序实数对
成立?若存在,求出所有符合条件的有序实数对 ,若不存在,请说明理由.
,若不存在,请说明理由.
已知:如图,在等腰梯形 中,
中, ,过点
,过点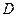 作
作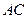 的平行线
的平行线 ,交
,交 的延长线于点
的延长线于点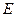 .求证:⑴
.求证:⑴ ⑵
⑵ 

已知: ,求证:
,求证: .
.
在直角坐标系xOy中,椭圆C1: 的左、右焦点分别为F1、F2.F2也是抛物线C2:
的左、右焦点分别为F1、F2.F2也是抛物线C2: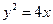 的焦点,点M为C1与C2在第一象限的交点,且
的焦点,点M为C1与C2在第一象限的交点,且 .
.
(Ⅰ)求C1的方程;
(Ⅱ)平面上的点N满足 ,直线l∥MN,且与C1交于A、B两点,若
,直线l∥MN,且与C1交于A、B两点,若 ·
·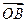 =0,求直线l的方程.
=0,求直线l的方程.
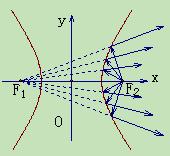
阅读下列材料,解决数学问题.圆锥曲线具有非常漂亮的光学性质,被人们广泛地应用于各种设计之中,比如椭圆镜面用来制作电影放映机的聚光灯,抛物面用来制作探照灯等,它们的截面分别是椭圆和抛物线.双曲线也具有非常好的光学性质,从双曲线的一个焦点发出的光线,经过双曲线反射后,反射光线是发散的,它们好像是从另一个焦点射出的一样,如图(1)所示.反比例函数 的图像是以直线
的图像是以直线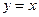 为轴,以坐标轴为渐近线的等轴双曲线,记作C.
为轴,以坐标轴为渐近线的等轴双曲线,记作C.
(Ⅰ)求曲线C的离心率及焦点坐标;
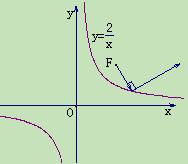
(Ⅱ)如图(2),从曲线C的焦点F处发出的光线经双曲线反射后得到的反射光线与入射光线垂直,求入射光线的方程.
(1) (2)
(2)
设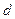 为非零实数,
为非零实数,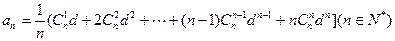
(Ⅰ)写出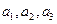 并判断
并判断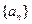 是否为等比数列.若是,给出证明;若不是,说明理由;
是否为等比数列.若是,给出证明;若不是,说明理由;
(Ⅱ)设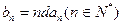 ,求数列
,求数列 的前n项和
的前n项和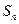 .
.