因式分解
(1)3ax+6ay
(2)25m2﹣4n2
(3)3a2+a﹣10
(4)ax2+2a2x+a3
(5)x3+8y3
(6)b2+c2﹣2bc﹣a2
(7)(a2﹣4ab+4b2)﹣(2a﹣4b)+1
(8)(x2﹣x)(x2﹣x﹣8)+12.
因式分解:
(1)﹣4a3b2+10a2b﹣2ab;
(2)6(x+y)2﹣2(x+y);
(3)﹣7ax2+14axy﹣7ay2;
(4)25(a﹣b)2﹣16(a+b)2;
(5)(x2+y2)2﹣4x2y2;
(6)a2+2ab+b2﹣1.
分解因式: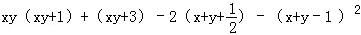 .
.
将下列各式因式分解:
(1)a3﹣16a;
(2)4ab+1﹣a2﹣4b2.
(3)9(a﹣b)2+12(a2﹣b2)+4(a+b)2;
(4)x2﹣2xy+y2+2x﹣2y+1.
(5)(x2﹣2x)2+2x2﹣4x+1.
(6)49(x﹣y)2﹣25(x+y)2
(7)81x5y5﹣16xy
(8)(x2﹣5x)2﹣36.
因式分解: .
.