（本小题满分12分）2014年7月16日，中国互联网络信息中心发布《第三十四次中国互联网发展状况报告》，报告显示：我国网络购物用户已达
亿．为了了解网购者一次性购物金额情况，某统计部门随机抽查了6月1日这一天100名网购者的网购情况，得到如下数据统计表．已知网购金额在2000元以上（不含2000元）的频率为
．
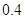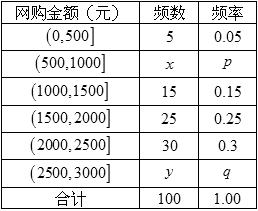
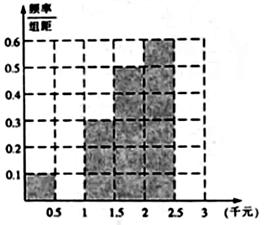
（1）确定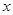
，
，
，
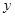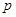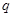的值，并补全频率分布直方图；
（2）为进一步了解网购金额的多少是否与网龄有关，对这100名网购者调查显示：购物金额在2000元以上的网购者中网龄3年以上的有35人，购物金额在2000元以下（含2000元）的网购者中网龄不足3年的有20人．
①请将列联表补充完整；
| |
网龄3年以上 |
网龄不足3年 |
合计 |
| 购物金额在2000元以上 |
35 |
|
|
| 购物金额在2000元以下 |
|
20 |
|
| 合计 |
|
|
100 |
②并据此列联表判断，是否有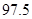
%的把握认为网购金额超过2000元与网龄在三年以上有关？
参考数据：
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
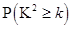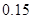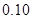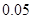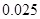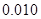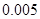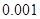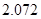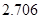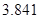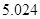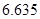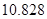（参考公式：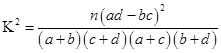
，其中
）
海面上相距10海里的A．B两船，B船在A船的北偏东45°方向上，两船同时接到指令同时驶向C岛，C岛在B船的南偏东75°方向上，行驶了80分钟后两船同时到达C岛，经测算，A船行驶了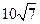
海里，求B船每小时的速度。
（本小题满分16分）已知数列
，其中数列是首项为2公比为
的等比数列，又
．
（Ⅰ）求数列
的通项公式；
（Ⅱ）求使不等式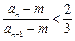
成立的所有正整数
的值．
（本小题满分16分）
已知函数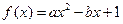
，
（Ⅰ）是否存在实数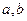
使
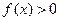的解集是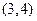
，若存在，求实数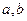的值，若不存在请说明理由．
（Ⅱ）若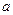
，
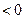，且不等式
在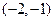
上恒成立，求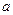的取值范围．
（本小题满分15分）数列
的前
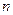项和为
，
，
．
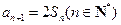（Ⅰ）求数列的通项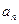
；（Ⅱ）求数列
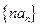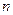的前项和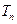
．
（本小题满分15分）
如图，某单位用木料制作如图所示的框架,框架的下部是边长分别为
(单位:米)的矩形,上部是斜边长为
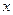的等腰直角三角形，要求框架围成的总面积为8平方米.
（Ⅰ）求的关系式，并求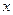的取值范围；
（Ⅱ）问分别为多少时用料最省?