如图,四边形ABCD为矩形,四边形ADEF为梯形,FE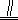
 AD,∠AFE=60°,且平面ABCD⊥平面ADEF,AF=FE=AB=2,点G为AC的中点.
AD,∠AFE=60°,且平面ABCD⊥平面ADEF,AF=FE=AB=2,点G为AC的中点.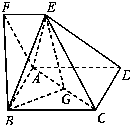
(Ⅰ)求证:EG∥平面ABF;
(Ⅱ)求三棱锥B﹣AEG的体积.
已知 、
、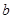 、
、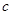 分别是
分别是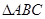 的三个内角
的三个内角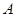 、
、 、
、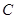 所对的边;
所对的边;
(1)若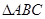 面积
面积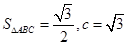 ,且
,且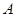 、
、 、
、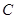 成等差数列,求
成等差数列,求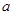 、
、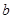 的值;
的值;
(2)若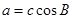 ,且
,且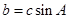 ,试判断
,试判断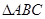 的形状。
的形状。
已知等差数列 中,
中,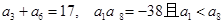 .
.
(Ⅰ)求 的通项公式;
的通项公式;
(Ⅱ)调整数列 的前三项
的前三项 的顺序,使它成为等比数列
的顺序,使它成为等比数列 的前三项,求
的前三项,求 的前
的前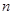 项和.
项和.
(本小题满分12分)
已知
(1)求 的值;
的值;
(2)当 (其中
(其中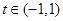 ,且
,且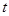 为常数)时,
为常数)时,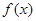 是否存在最小值,如果存在求出最小值;如
是否存在最小值,如果存在求出最小值;如
果不存在,请说明理由;
(3)当 时,求满足不等式
时,求满足不等式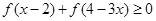 的
的 的范围.
的范围.
已知定义域为(0,+∞)的函数f(x)满足:
①x>1时,f(x)<0,②f( )=1,③对任意x,y
)=1,③对任意x,y ( 0,+∞),
( 0,+∞),
都有f(xy)= f(x)+ f(y),求不等式f(x)+ f(5-x)≥-2的解集。
已知函数 =
=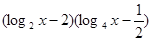 ,2≤
,2≤ ≤4
≤4
(1)求该函数的值域;
(2)若 对于
对于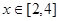 恒成立,求
恒成立,求 的取值范围.
的取值范围.