已知动圆Q过定点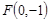 ,且与直线
,且与直线 相切,椭圆
相切,椭圆 的对称轴为坐标轴,
的对称轴为坐标轴, 点为坐标原点,
点为坐标原点, 是其一个焦点,又点
是其一个焦点,又点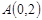 在椭圆
在椭圆 上.
上.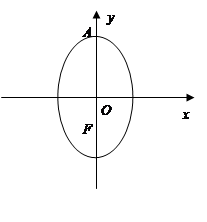
(Ⅰ)求动圆圆心 的轨迹
的轨迹 的标准方程和椭圆
的标准方程和椭圆 的标准方程;
的标准方程;
(Ⅱ)若过 的动直线
的动直线 交椭圆
交椭圆 于
于 点,交轨迹
点,交轨迹 于
于 两点,设
两点,设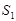 为
为 的面积,
的面积, 为
为 的面积,令
的面积,令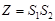 ,试求
,试求 的最小值.
的最小值.
△ABC中,D在边BC上,且BD=2,DC=1,∠B=60o,∠ADC=150o,求AC的长及△ABC的面积.
一货轮航行到M处,测得灯塔S在货轮北偏东15º相距20海里处,随后货轮按北偏西30º的方向航行,半小时后,又测得灯塔在北偏东45º,求货轮的速度。
已知点B(1,0)是向量a的终点,向量b, c均以原点O为起点,且b=(-3,-4), c=(1,1)与向量a的关系为a=3b-2c,求向量a的起点坐标.
(本小题满分14分)
如图,在五棱锥P—ABCDE中,PA⊥平面ABCDE,AB∥CD,AC∥ED,AE∥BC, 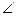 ABC=45°,AB=2
ABC=45°,AB=2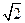 ,BC=2AE=4,三角形PAB是等腰三角形.
,BC=2AE=4,三角形PAB是等腰三角形.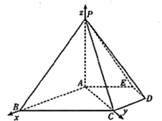
(I)求证:平面PCD⊥平面PAC;
(II)求四棱锥P—ACDE的体积.
(本小题满分12分)
如图所示,在正方体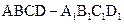 中,E是棱
中,E是棱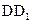 的中点.
的中点.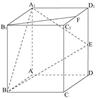
(Ⅰ)求直线BE与平面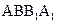 所成的角的正弦值;
所成的角的正弦值;
(Ⅱ)在棱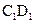 上是否存在一点F,使
上是否存在一点F,使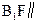 平面
平面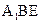 ?证明你的结论.
?证明你的结论.