(本小题满分10分)选修4—4:坐标系与参数方程
在平面直角坐标系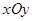 中,圆
中,圆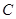 的参数方程为
的参数方程为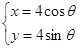 (
( 为参数),直线
为参数),直线 经过点
经过点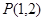 ,倾斜角
,倾斜角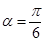 .
.
(1)写出圆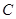 的标准方程和直线
的标准方程和直线 的参数方程;
的参数方程;
(2)设直线 与圆
与圆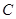 相交于
相交于 ,
,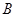 两点,求
两点,求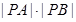 的值.
的值.
(本小题满分12分)设椭圆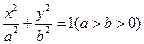 的焦点分别为
的焦点分别为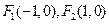 ,
,
直线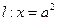 交
交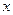 轴于于点A,且
轴于于点A,且 。
。
(1)试求椭圆的方程;
(2)过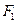 、
、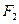 分别作互相垂直的两直线与椭圆分别
分别作互相垂直的两直线与椭圆分别
交于D、E、M、N四点(如图所示),若四边形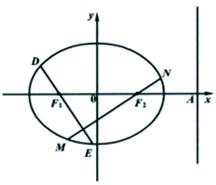
DMEN的面积为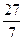 ,求DE的直线方程。
,求DE的直线方程。
(本小题满分12分)如图所示,正方形A BCD与直角梯形ADEF所
BCD与直角梯形ADEF所
在平面互相 垂直,∠ADE=90°,AF∥DE,DE=DA=2AF=2。
垂直,∠ADE=90°,AF∥DE,DE=DA=2AF=2。
(1)求证:AC∥平面BEF;
(2)求四面体BDEF的体积。
(本小题满分12分)品厂为了检查甲、乙两条自动包装流水线的生产情况,在这两条
流水线上各抽取40件产品作为样本称 出它们的重量(单位:克),重量值落在(495,510]
出它们的重量(单位:克),重量值落在(495,510]
的产 品为合格品,否则为不合格品,表1是甲流水线样本频数分布表,
品为合格品,否则为不合格品,表1是甲流水线样本频数分布表, 图1是乙流水线样
图1是乙流水线样
本的频率分布直方图。 某食
某食
(1)若检验员不小心将甲、乙两条流水线生产的重量值在(510,515]的产品放在了一起,
然后又随机取出3件产品,求至少有一件是乙流水线生产的产品的概率;
(2)由以上统计数据完成下面2×2列联表,并回答有多大的把握认为“产品的包装质量
与两条自动包装流水线的选择有关”。
| 甲流水线 |
乙流水线 |
合计 |
|
| 合格品 |
a= |
b= |
|
| 不合格品 |
c= |
d= |
|
| 合计 |
n= |
(本小题满分12分)已知向量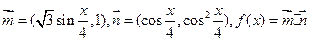 。
。
(1)若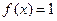 ,求
,求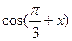 的值;
的值;
(2)在△ABC中,角A、B、C的对边分别是a、b、c,且满足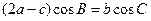 ,
,
求函数 的取值范围。
的取值范围。
已知构成某系统的元件能正常工作的概率为p(0<p<1),且各个元件能否正常工作是相互独立的.今有2n(n大于1)个元件可按下图所示的两种联结方式分别构成两个系统甲、乙.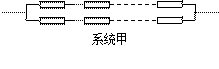
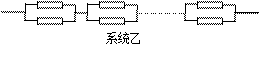
(1)试分别求出系统甲、乙能正常工作的概率p1,p2;
(2)比较p1与p2的大小,并从概率意义上评价两系统的优劣.