(本小题满分12分)已知数列 是各项均为正数的等差数列,其中
是各项均为正数的等差数列,其中 ,且
,且 成等比数列;数列
成等比数列;数列 的前
的前 项和为
项和为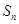 ,满足
,满足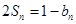 .
.
(Ⅰ)求数列 ,
, 的通项公式;
的通项公式;
(Ⅱ)如果 ,设数列
,设数列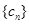 的前
的前 项和为
项和为 ,是否存在正整数
,是否存在正整数 ,使得
,使得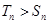 成立,若存在,求出
成立,若存在,求出 的最小值,若不存在,说明理由.
的最小值,若不存在,说明理由.
求函数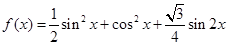 .
.
(1)求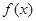 的周期与值域;
的周期与值域;
(2)求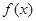 在
在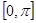 上的单调递减区间.
上的单调递减区间.
设函数 f (x)=ax-lnx-3(a∈R),g(x)=xe1-x.
(Ⅰ)若函数 g(x) 的图象在点 (0,0) 处的切线也恰为 f (x) 图象的一条切线,求实数a的值;
(Ⅱ)是否存在实数a,对任意的 x∈(0,e],都有唯一的 x0∈[e-4,e],使得 f (x0)=g(x) 成立.若存在,求出a的取值范围;若不存在,请说明理由.
注:e是自然对数的底数.
已知椭圆C: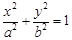 (a>0,b>0)的离心率为
(a>0,b>0)的离心率为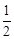 ,以原点为圆心,椭圆的短半轴为半径的圆与直线x-y+
,以原点为圆心,椭圆的短半轴为半径的圆与直线x-y+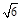 =0相切.又设P(4,0),A,B是椭圆C上关于x轴对称的任意两个不同的点,连结PB交椭圆C于另一点E.
=0相切.又设P(4,0),A,B是椭圆C上关于x轴对称的任意两个不同的点,连结PB交椭圆C于另一点E.
(Ⅰ)求椭圆C的方程;
(Ⅱ)证明:直线AE与x轴相交于定点Q;
(III)求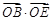 的取值范围.
的取值范围.
若将边长为2的正方形ABCD沿对角线BD折成一个直二面角,且EA⊥平面ABD,AE=a(如图).
(Ⅰ)若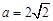 ,求证:AB//平面CDE;
,求证:AB//平面CDE;
(Ⅱ)求实数a的值,使得二面角A-EC-D的大小为60°.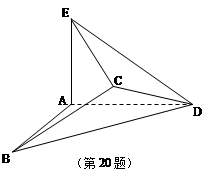
设数列 {an} 中,a1=a,an+1+2an=2n+1(n∈N*).
(Ⅰ)若a1,a2,a3成等差数列,求实数a的值;
(Ⅱ)试问数列 {an} 能为等比数列吗?若能,试写出它的充要条件并加以证明;若不能,请说明理由.