(本小题满分12分)2015年3月15日,中央电视台揭露部分汽车4S店维修黑幕,国家工商总局针对汽车制造行业中的垄断行为加大了调查力度,对汽车零部件加工的相关企业开出了巨额罚单.某品牌汽车制造商为了压缩成本,计划对 、
、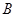 、
、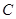 三种汽车零部件进行招标采购,某著名汽车零部件加工厂参入了该次竞标,已知
三种汽车零部件进行招标采购,某著名汽车零部件加工厂参入了该次竞标,已知 种零部件中标后即可签合同,而
种零部件中标后即可签合同,而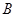 、
、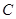 两种汽车零部件具有很强的关联性,所以公司规定两者都中标才能签合同,否则都不签合同,而三种零部件是否中标互不影响.已知该汽车零部件加工厂中标
两种汽车零部件具有很强的关联性,所以公司规定两者都中标才能签合同,否则都不签合同,而三种零部件是否中标互不影响.已知该汽车零部件加工厂中标 种零部件的概率为
种零部件的概率为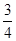 ,只中标
,只中标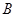 种零部件的概率为
种零部件的概率为 ,
,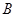 、
、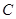 两种零部件签订合同的概率为
两种零部件签订合同的概率为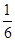 .
.
(Ⅰ)求该汽车零部件加工厂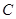 种汽车零部件中标的概率;
种汽车零部件中标的概率;
(Ⅱ)设该汽车零部件加工厂签订合同的汽车零部件种数为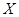 ,求
,求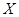 的分布列与期望.
的分布列与期望.
(本小题满分10分)选修4-4:坐标系与参数方程:
以直角坐标系的原点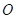 为极点,
为极点,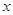 轴的正半轴为极轴,且两个坐标系取相等的长度单位.已知直线
轴的正半轴为极轴,且两个坐标系取相等的长度单位.已知直线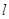 的参数方程为
的参数方程为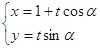 (
(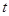 为参数,
为参数, ),曲线
),曲线 的极坐标方程为
的极坐标方程为 .
.
(Ⅰ)求曲线 的直角坐标方程;
的直角坐标方程;
(Ⅱ)设直线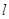 与曲线
与曲线 相交于
相交于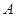 、
、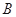 两点,当
两点,当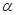 变化时,求
变化时,求 的最小值.
的最小值.
(本小题满分10分)选修4-1:几何证明选讲:
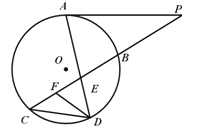
如图所示,已知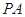 与⊙
与⊙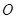 相切,
相切,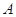 为切点,过点
为切点,过点 的割线交圆于
的割线交圆于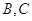 两点,弦
两点,弦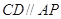 ,
,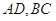 相交于点
相交于点 ,
, 为
为 上一点,且
上一点,且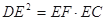 .
.
(Ⅰ)求证: ;
;
(Ⅱ)若 ,求
,求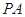 的长.
的长.
(本小题满分12分) 设函数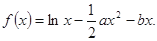
(1)当 时,求函数
时,求函数 的单调区间;
的单调区间;
(2)令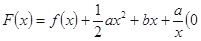 <
< ≤
≤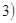 ,其图像上任意一点
,其图像上任意一点 处切线的斜率
处切线的斜率 ≤
≤ 恒成立,求实数
恒成立,求实数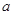 的取值范围;
的取值范围;
(3)当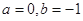 时,方程
时,方程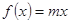 在区间
在区间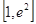 内有唯一实数解,求实数
内有唯一实数解,求实数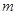 的取值范围.
的取值范围.
(本小题满分12分)椭圆 :
: 的离心率为
的离心率为 ,长轴端点与短轴端点间的距离为
,长轴端点与短轴端点间的距离为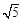 .
.
(1)求椭圆 的方程;
的方程;
(2)设过点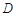
 的直线
的直线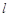 与椭圆
与椭圆 交于
交于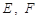 两点,
两点, 为坐标原点,若
为坐标原点,若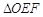 为直角三角形,求直线
为直角三角形,求直线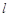 的斜率.
的斜率.
(本小题满分12分)在如图所示的空间几何体中,平面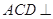 平面
平面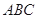 ,
,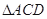 与
与 是边长为
是边长为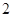 的等边三角形,
的等边三角形,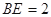 ,
, 和平面
和平面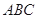 所成的角为
所成的角为 ,且点
,且点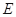 在平面
在平面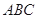 上的射影落在
上的射影落在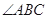 的平分线上.
的平分线上.
(Ⅰ)求证: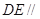 平面
平面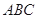 ;
;
(Ⅱ)求二面角 的余弦值.
的余弦值.