（本小题满分12分）根据我国发布了新修订的《环境空气质量标准》指出空气质量指数在
为优秀，人类可正常活动．某市环保局对该市2014年进行为期一年的空气质量监测，得到每天的空气质量指数，从中随机抽取50个作为样本进行分析报告，样本数据分组区间为
，
， 
， 
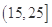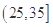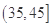，由此得到样本的空气质量指数频率分布直方图．
（Ⅰ）若空气质量指数大于或等于15且小于35认为是良好的，求该市在这次监测中空气质量
为良好的天数，并根据频率分布直方图估计这一年度的空气质量指数的平均值；
（Ⅱ）如果空气质量指数不超过15，就认定空气质量为“优”，则从这一年的监测数据中随机
抽取3天的数值，其中达到“优”的天数为
，求的分布列和数学期望．
如图，两矩形ABCD，ABEF所在平面互相垂直，DE与平面ABCD及平面ABEF所成角分别为
，M、N分别为DE与DB的中点，且MN=1.
(1) 求证：MN丄平面ABCD
(2) 求线段AB的长；
(3) 求二面角A—DE—B的平面角的正弦值.
设函数
，若函数在点
处的切线为
，数列
定义：
。
（1）求实数
的值；
（2）若将数列
的前
项的和与积分别记为
。证明：对任意正整数，
为定值；证明：对任意正整数，都有
。
已知
分别是双曲线
的左、右焦点，过
斜率为
的直线
交双曲线的左、右两支分别于
两点，过
且与垂直的直线
交双曲线的左、右两支分别于
两点。
（1）求的取值范围；
求四边形
面积的最小值。
已知函数
，其中
为常数。
（1）若
在（0，1）上单调递增，求实数的取值范围；
（2）求证：
。
为了参加广州亚运会，从四支较强的排球队中选出18人组成女子排球国家队，队员来源人数如下表：
| 队别 |
北京 |
上海 |
天津 |
八一 |
| 人数 |
4 |
6 |
3 |
5 |
（1）从这18名队员中随机选出两名，求两人来自同一支队的概率；
（2）中国女排奋力拼搏，战胜韩国队获得冠军．若要求选出两位队员代表发言，设其中来自北京队的人数为
，求随机变量
的分布列及数学期望
．