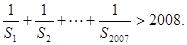(本小题满分14分)设函数 (
( ).
).
(1)当 时,求过点
时,求过点 且与曲线
且与曲线 相切的切线方程;
相切的切线方程;
(2)求函数 的单调递增区间;
的单调递增区间;
(3)若函数 有两个极值点
有两个极值点 ,
, ,且
,且 ,记
,记 表示不大于
表示不大于 的最大整数,试比较
的最大整数,试比较 与
与 的大小.
的大小.
2011年深圳大运会,某运动项目设置了难度不同的甲、乙两个系列,每个系列都有K和D两个动作,比赛时每位运动员自选一个系列完成,两个动作得分之和为该运动员的成绩。假设每个运动员完成每个系列中的两个动作的得分是相互独立的,根据赛前训练统计数据,某运动员完成甲系列和乙系列的情况如下表:
甲系列:
| 动作 |
K |
D |
||
| 得分 |
100 |
80 |
40 |
10 |
| 概率 |
 |
 |
 |
 |
乙系列:
| 动作 |
K |
D |
||
| 得分 |
90 |
50 |
20 |
0 |
| 概率 |
 |
 |
 |
 |
现该运动员最后一个出场,其之前运动员的最高得分为118分。
(I)若该运动员希望获得该项目的第一名,应选择哪个系列,说明理由,并求其获得第一名的概率;
(II)若该运动员选择乙系列,求其成绩X的分布列及其数学期望EX
一个四棱锥的三视图如图所示,E为侧棱PC上一动点。
(1)画出该四棱锥的直观图,并指出几何体的主要特征(高、底等).
(2)点 在何处时,
在何处时, 面EBD,并求出此时二面角
面EBD,并求出此时二面角 平面角的余弦值
平面角的余弦值
已知等差数列 满足:
满足: ,
, ,
, 的前n项和为
的前n项和为 .
.
(Ⅰ)求 及
及 ;
;
(Ⅱ)令bn=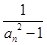 (
( ),求数列
),求数列 的前n项和
的前n项和 。
。
已知向量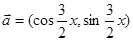 ,
, ,且
,且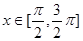
(1)求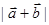 的取值范围;
的取值范围;
(2)求函数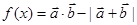 的最小值,并求此时x的值
的最小值,并求此时x的值
设等差数列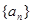 的公差
的公差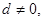 且
且 记
记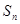 为数列
为数列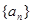 的前
的前 项和.
项和.
(1)若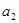 、
、 、
、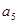 成等比数列,且
成等比数列,且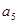 、
、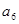 的等差中项为
的等差中项为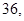 求数列
求数列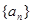 的通项公式;
的通项公式;
(2)若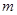 、
、 、
、 且
且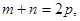 证明:
证明: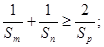
(3)若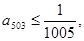 证明:
证明: