(本小题满分12分)如图,四边形ABCD为梯形,AB∥CD, 平面ABCD,
平面ABCD, ,
,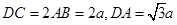 ,E为BC中点.
,E为BC中点.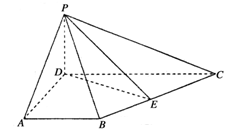
(1)求证:平面 平面PDE;
平面PDE;
(2)线段PC上是否存在一点F,使PA//平面BDF?若有,请找出具体位置,并进行证明;若无,请分析说明理由.
已知△ABC的内角A、B、C所对的边分别为 ,且
,且 , cosB=
, cosB= .
.
(1) 若b=4,求sinA的值;
(2) 若△ABC的面积S△ABC=4,求b,c的值.
已知数列 的前n项和为
的前n项和为 且
且 ,数列
,数列 满足
满足 且
且
 .
.
(1)求 的通项公式;
的通项公式;
(2)求证:数列 为等比数列;
为等比数列;
(3)求 前n项和.
前n项和.
已知A、B、C是直线 上的不同三点,O是
上的不同三点,O是 外一点,向量
外一点,向量 满足
满足 ,记
,记 ;
;
(1)求函数 的解析式;
的解析式;
(2)求函数 的单调区间.
的单调区间.
等比数列{ }的前n项和为
}的前n项和为 ,已知对任意的
,已知对任意的 ,点
,点 ,均在函数
,均在函数 且
且 均为常数)的图像上.
均为常数)的图像上.
(1)求r的值;
(2)当b=2时,记  求数列
求数列 的前
的前 项和
项和 .
.
已知 ,且
,且 .
.
(1)将 表示为
表示为 的函数
的函数 ,并求
,并求 的单调增区间;
的单调增区间;
(2)已知 分别为
分别为 的三个内角
的三个内角 对应的边长,若
对应的边长,若 ,求
,求 的面积.
的面积.