(文科)已知椭圆
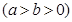 的右焦点为
的右焦点为
 ,短轴的端点分别为
,短轴的端点分别为 ,且
,且 .
.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)过点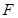 且斜率为
且斜率为
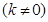 的直线
的直线 交椭圆于
交椭圆于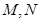 两点,弦
两点,弦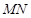 的垂直平分线与
的垂直平分线与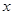 轴相交于点
轴相交于点 .设弦
.设弦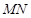 的中点为
的中点为 ,试求
,试求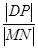 的取值范围.
的取值范围.
已知函数f(x)=x-xlnx , ,其中
,其中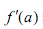 表示函数f(x)在
表示函数f(x)在
x=a处的导数,a为正常数.
(1)求g(x)的单调区间;
(2)对任意的正实数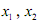 ,且
,且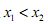 ,证明:
,证明:
(3)对任意的
如图6,已知动圆M过定点F(1,0)且与x轴相切,点F 关于圆心M 的对称点为 F',动点F’的轨迹为C.
(1)求曲线C的方程;
(2)设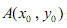 是曲线C上的一个定点,过点A任意作两条倾斜角互补的直线,分别与曲线C相交于另外两点P 、Q.
是曲线C上的一个定点,过点A任意作两条倾斜角互补的直线,分别与曲线C相交于另外两点P 、Q.
①证明:直线PQ的斜率为定值;
②记曲线C位于P 、Q两点之间的那一段为l.若点B在l上,且点B到直线PQ的
距离最大,求点B的坐标.
已知数列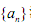 满足:
满足: ,且
,且
(1)求通项公式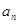
(2)设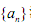 的前n项和为S n,问:是否存在正整数m、n,使得
的前n项和为S n,问:是否存在正整数m、n,使得
若存在,请求出所有的符合条件的正整数对(m,n),若不存在,请说明理由.
如图 5,已知正方形ABCD在水平面上的正投影(投影线垂直于投影面)是四边形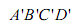 ,其中A与A '重合,且BB'<DD'<CC'.
,其中A与A '重合,且BB'<DD'<CC'.
(1)证明AD'//平面BB'C'C,并指出四边形AB'C'D’的形状;
(2)如果四边形中AB'C'D’中, ,正方形的边长为
,正方形的边长为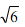 ,
,
求平面ABCD与平面AB'C'D’所成的锐二面角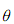 的余弦值.
的余弦值.
深圳市某校中学生篮球队假期集训,集训前共有6个篮球,其中3个是新球(即没有用过的球), 3 个是旧球(即至少用过一次的球).每次训练,都从中任意取出2 个球,用完后放回.
(1)设第一次训练时取到的新球个数为 ,求
,求 的分布列和数学期望;
的分布列和数学期望;
(2)求第二次训练时恰好取到一个新球的概率.