(本小题满分12分)已知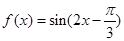 ,
,
(1)函数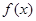 的图象可以由函数
的图象可以由函数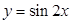 的图象经过怎样的变换得到?
的图象经过怎样的变换得到?
(2)若方程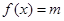 在
在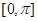 上有两个不等实根,求
上有两个不等实根,求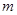 的取值范围;
的取值范围;
(3)在(2)的条件下,求方程的两实根之和。
设平面向量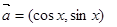 ,
, ,函数
,函数 .
.
(Ⅰ)求函数 的值域和函数的单调递增区间;
的值域和函数的单调递增区间;
(Ⅱ)当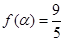 ,且
,且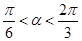 时,求
时,求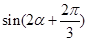 的值.
的值.
已知函数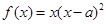 ,
,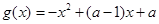 (其中
(其中 为常数);
为常数);
(Ⅰ)如果函数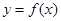 和
和 有相同的极值点,求
有相同的极值点,求 的值;
的值;
(Ⅱ)设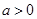 ,问是否存在
,问是否存在 ,使得
,使得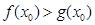 ,若存在,请求出实数
,若存在,请求出实数 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
(Ⅲ)记函数 ,若函数
,若函数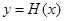 有5个不同的零点,求实数
有5个不同的零点,求实数 的取值范围.
的取值范围.
已知函数 .
.
(Ⅰ)若 ,且对于任意
,且对于任意 恒成立,试确定实数
恒成立,试确定实数 的取值范围;
的取值范围;
(Ⅱ)设函数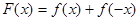 ,求证:
,求证: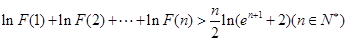
数列{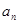 }的前n项和为
}的前n项和为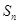 ,
, .
.
(Ⅰ)设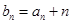 ,证明:数列
,证明:数列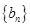 是等比数列;
是等比数列;
(Ⅱ)求数列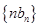 的前
的前 项和
项和 ;
;
(Ⅲ)若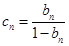 ,数列
,数列 的前
的前 项和
项和 ,证明:
,证明: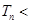
 .
.
某校从参加高二年级学业水平测试的学生中抽出80名学生,其数学成绩(均为整数)的频率分布直方图如图所示.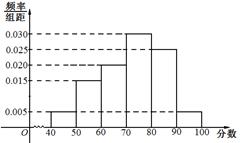
(I)估计这次测试数学成绩的平均分;
(II)假设在[90,100]段的学生的数学成绩都不相同,且都超过94分.若将频率视为概率,现用简单随机抽样的方法,从95,96,97,98,99,100这6个数中任意抽取2个数,有放回地抽取了3次,记这3次抽取中,恰好是两个学生的数学成绩的次数为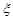 ,求
,求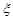 的分布列及数学期望
的分布列及数学期望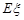 .
.