已知以原点
为中心的椭圆的一条准线方程为
,离心率
,
是椭圆上的动点.
(Ⅰ)若
的坐标分别是
,求
的最大值;
(Ⅱ)如图,点
的坐标为
,
是圆
上的点,
是点
在
轴上的射影,点
满足条件:
,求线段
的中点
的轨迹方程.

在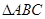 中,
中,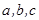 分别是角A、B、C的对边,
分别是角A、B、C的对边, 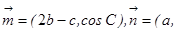
 ,且
,且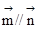 .
.
(1)求角A的大小;
(2)求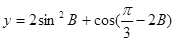 的值域.
的值域.
已知点A(-1,0),B(1,-1)和抛物线.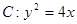 ,O为坐标原点,过点A的动直线l交抛物线C于M、P,直线MB交抛物线C于另一点Q,如图.
,O为坐标原点,过点A的动直线l交抛物线C于M、P,直线MB交抛物线C于另一点Q,如图.
(1)证明:  为定值;
为定值;
(2)若△POM的面积为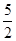 ,求向量
,求向量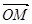 与
与 的夹角;
的夹角;
(3)证明直线PQ恒过一个定点.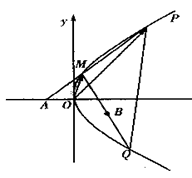
对于三次函数
 。
。
定义:(1)设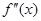 是函数
是函数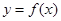 的导数
的导数 的导数,若方程
的导数,若方程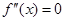 有实数解
有实数解 ,则称点
,则称点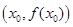 为函数
为函数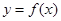 的“拐点”;
的“拐点”;
定义:(2)设 为常数,若定义在
为常数,若定义在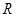 上的函数
上的函数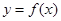 对于定义域内的一切实数
对于定义域内的一切实数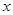 ,都有
,都有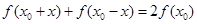 成立,则函数
成立,则函数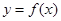 的图象关于点
的图象关于点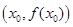 对称。
对称。
己知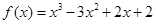 ,请回答下列问题:
,请回答下列问题:
(1)求函数 的“拐点”
的“拐点”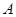 的坐标
的坐标
(2)检验函数 的图象是否关于“拐点”
的图象是否关于“拐点”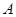 对称,对于任意的三次函数写出一个有关“拐点”的结论(不必证明)
对称,对于任意的三次函数写出一个有关“拐点”的结论(不必证明)
(3)写出一个三次函数 ,使得它的“拐点”是
,使得它的“拐点”是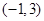 (不要过程)
(不要过程)
已知等差数列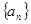 的前n项和为
的前n项和为 ,公差
,公差
 成等比数列
成等比数列
(1)求数列 的通项公式;
的通项公式;
(2)若从数列 中依次取出第2项、第4项、第8项,
中依次取出第2项、第4项、第8项, ,按原来顺序组成一个新数列
,按原来顺序组成一个新数列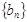 ,且这个数列的前
,且这个数列的前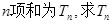 的表达式.
的表达式.
甲、乙两人玩一种游戏;在装有质地、大小完全相同,编号分别为1,2,3,4,5,6六个球的口袋中,甲先模出一个球,记下编号,放回后乙再模一个球,记下编号,如果两个编号的和为偶数算甲赢,否则算乙赢.
(1)求甲赢且编号和为8的事件发生的概率;
(2)这种游戏规则公平吗?试说明理由.