8分,观察下列各式及其验证过程: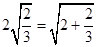
验证:
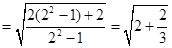 .
.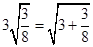
验证: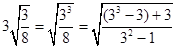

(1)按照上述两个等式及其验证过程的基本思路,猜想 的变形结果并进行验证;
的变形结果并进行验证;
(2)针对上述各式反映的规律,写出用n(n为任意自然数,且n≥2)表示的等式,并给出证明.
如图,在梯形ABCD中,AD∥BC,AB=AD,∠BAD的平分线AE 交BC于E, EC=AB, F、G分别是AB、AD的中点.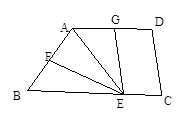
求证:(1)△AGE≌AFE;
(2)EF=CD.
解方程或不等式组(每小题4分,共8分)(1)
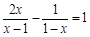
(2)
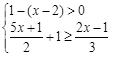
如图, 为直角三角形,
为直角三角形, ,
, ,
, ;四边形
;四边形 为矩形,
为矩形, ,
, ,且点
,且点 、
、 、
、 、
、 在同一条直线上,点
在同一条直线上,点 与点
与点 重合.
重合.
(1)求边
 的长;
的长;(2)将
 以每秒
以每秒 的速度沿矩形
的速度沿矩形 的边
的边 向右平移,当点
向右平移,当点 与点
与点 重合时停止移动,设
重合时停止移动,设 与矩形
与矩形 重叠部分的面积为
重叠部分的面积为 ,请求出重叠部分的面积
,请求出重叠部分的面积 (
( )与移动时间
)与移动时间 的函数关系式(时间不包含起始与终止时刻);
的函数关系式(时间不包含起始与终止时刻);(3)在(2)的基础上,当
 移动至重叠部分的面积为
移动至重叠部分的面积为
 时,将
时,将 沿边
沿边 向上翻折,得到
向上翻折,得到 ,请求出
,请求出 与矩形
与矩形 重叠部分的周长(可利用备用图).
重叠部分的周长(可利用备用图).
有一座抛物线型拱桥,其水面宽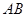 为18米,拱顶
为18米,拱顶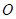 离水面
离水面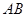 的距离
的距离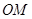 为8米,货船在水面上的部分的横断面是矩形
为8米,货船在水面上的部分的横断面是矩形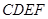 ,如图建立平面直角坐标系.
,如图建立平面直角坐标系.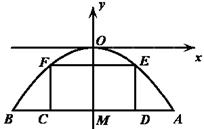
(1)求此抛物线的解析式,并写出自变量的取值范围;
(2)如果限定
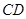 的长为9米,
的长为9米,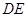 的长不能超过多少米,才能使船通过拱桥?
的长不能超过多少米,才能使船通过拱桥?(3)若设
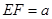 ,请将矩形
,请将矩形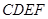 的面积
的面积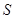 用含
用含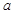 的代数式表示,并指出
的代数式表示,并指出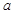 的取值范围.
的取值范围.
一次函数 的图象经过点
的图象经过点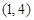 ,且分别与
,且分别与 轴、
轴、 轴交于点
轴交于点 、
、 .
.
点
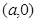 在
在 轴正半轴上运动,点
轴正半轴上运动,点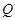
 在
在 轴正半轴上运动,且
轴正半轴上运动,且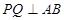 .
.(1)求
 的值,并在给出的平面直角坐标系中画出该一次函数的图象;
的值,并在给出的平面直角坐标系中画出该一次函数的图象;(2)求
 与
与 满足的等量关系式.
满足的等量关系式.