(本小题满分16分)如图,等腰梯形 的三边
的三边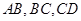 分别与函数
分别与函数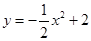 ,
,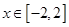 的图象切于点
的图象切于点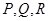 .求梯形
.求梯形 面积的最小值.
面积的最小值.
已知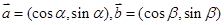 .
.
(1)若 ,求
,求 的值;
的值;
(2)若 ,且
,且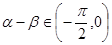 ,求
,求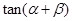 的值.
的值.
已知 为等差数列,且
为等差数列,且 ,公差
,公差 .
.
(1)数列满足结论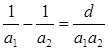 ;
;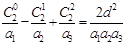 ;试证:
;试证: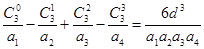 ;
;
(2)根据(1)中的几个等式,试归纳出更一般的结论,并用数学归纳法证明.
【原创】甲、乙两人进行围棋比赛,约定先连胜两局者直接赢得比赛,若赛完5局仍未出现连胜,则判定获胜局数多者赢得比赛.假设每局甲获胜的概率为 ,乙获胜的概率为
,乙获胜的概率为 ,各局比赛结果相互独立.
,各局比赛结果相互独立.
(1)求甲在4局以内(含4局)赢得比赛的概率;
(2)记X为比赛决出胜负时的总局数,求X的分布列和均值(数学期望).
选修4 - 5:不等式选讲已知x,y,z均为正数.求证: .
.
在极坐标系中,圆 的方程为
的方程为 ,以极点为坐标原点,极轴为
,以极点为坐标原点,极轴为 轴的正半轴建立平面直角坐标系,直线
轴的正半轴建立平面直角坐标系,直线 的参数方程为
的参数方程为 (
( 为参数),若直线
为参数),若直线 与圆
与圆 相切,求实数
相切,求实数 的值.
的值.