(本小题满分16分)设函数f(x)=xsinx(x∈R),
(Ⅰ)证明f(x+2kπ)-f(x)=2kπsinx,其中k为整数;
(Ⅱ)设x0为f(x)的一个极值点,证明  ;
;
(提示 )
)
(Ⅲ)设f(x)在(0,+∞)内的全部极值点按从小到大的顺序排列a1,a2,,an,,证明 .
.
(本小题满分12分)
已知函数 和函数
和函数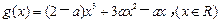
(Ⅰ)令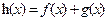 ,若函数h(x)在[1, +∞)上存在单调递减区间,求实数a的取值范围
,若函数h(x)在[1, +∞)上存在单调递减区间,求实数a的取值范围
(Ⅱ)当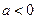 时,若
时,若 有极大值-7,求实数
有极大值-7,求实数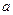 的值.
的值.
(本小题满分12分)
已知△ 的内角
的内角 所对的边分别为
所对的边分别为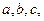 且
且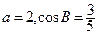 .
.
(Ⅰ)若 , 求
, 求 的值;
的值;
(Ⅱ)若△ 的面积
的面积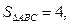 求
求 的值.
的值.
本小题满分12分)
设命题 :函数f(x)=x3-ax-1在区间
:函数f(x)=x3-ax-1在区间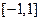 上单调递减;命题
上单调递减;命题 :函数
:函数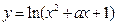 的定义域是
的定义域是 .如果命题
.如果命题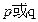 为真命题,
为真命题,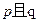 为假命题,求
为假命题,求 的取值范围.
的取值范围.
(本小题满分12分)
某矩形花园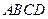 ,
,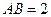 ,
, ,
, 是
是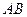 的中点,在该花园中有一花圃其形状是以
的中点,在该花园中有一花圃其形状是以 为直角顶点的内接Rt△
为直角顶点的内接Rt△ ,其中E、F分别落在线段
,其中E、F分别落在线段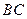 和线段
和线段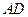 上如图.分别记
上如图.分别记 为
为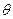 (
(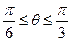 ),
), 的周长为
的周长为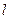 ,
, 的面积为
的面积为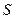 。
。
(1)试求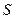 的取值范围;
的取值范围;
(2)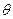 为何值时
为何值时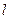 的值为最小;并求
的值为最小;并求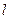 的最小值
的最小值

(本小题满分14分)
已知点A、B、C的坐标分别为A(3,0)、B(0,3)、C(cosα,sinα),α∈(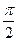 ,
, )。
)。
(1)若|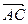 |=|
|=| |,求角α的值;
|,求角α的值;
(2)若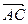 ·
·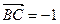 ,求
,求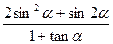 的值
的值