(本小题满分12分)如图,在四棱锥P-ABCD中,底面是直角梯形ABCD,其中AD⊥AB,CD∥AB,AB=4,CD=2,侧面PAD是边长为2的等边三角形,且与底面ABCD垂直,E为PA的中点.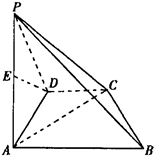
(Ⅰ)求证:DE∥平面PBC;
(Ⅱ)求三棱锥A-PBC的体积.
(本小题满分14分)
如图所示,在长方体 中,AB=AD=1,AA1=2,M是棱CC1的中点
中,AB=AD=1,AA1=2,M是棱CC1的中点
(Ⅰ)求异面直线A1M和C1D1所成的角的正切值;
(Ⅱ)证明:平面ABM⊥平面A1B1M1
(本小题满分14分)
已知圆C: ,是否存在斜率为1的直线l,使l被圆C截得的弦AB为直径的圆过原点,若存在,求出直线l的方程;若不存在说明理由。
,是否存在斜率为1的直线l,使l被圆C截得的弦AB为直径的圆过原点,若存在,求出直线l的方程;若不存在说明理由。
(本小题14分)已知圆C的圆心在直线 上,且与直线
上,且与直线 相切,被直线
相切,被直线 截得的弦长为
截得的弦长为 ,求圆C的方程.
,求圆C的方程.
(本小题满分12分)
为了比较注射A,B两种药物后产生的皮肤疱疹的面积,选200只家兔做实验,将这200只家兔随机地分成两组。每组100只,其中一组注射药物A,另一组注射药物B。下表1和表2分别是注射药物A和药物B后的实验结果。(疱疹面积单位: )
)
完成下面频率分布直方图,并比较注射两种药物后疱疹面积的中位数大小;
本小题满分12分)奇瑞公司生产的“奇瑞”轿车是我国民族品牌.该公司2009年生产的“旗云”、“风云”、“ ”三类经济型轿车中,每类轿车均有舒适和标准两种型号.某周产量如下表:
”三类经济型轿车中,每类轿车均有舒适和标准两种型号.某周产量如下表:
| 车型 |
旗云 |
风云 |
 |
| 舒适 |
100 |
150 |
 |
| 标准 |
300 |
 |
600 |
若按分层抽样的方法在这一周生产的轿车中抽取50辆进行检测,则必须抽取“旗云”轿车10辆,“风云”轿车15辆.
(1)求 、
、 的值;
的值;
(2)在年终促销活动中,奇瑞公司奖给了某优秀销售公司2辆舒适型和3辆标准型“ ”轿车,该销售公司又从中随机抽取了2辆作为奖品回馈消费者.求至少有一辆是舒适型轿车的概率.
”轿车,该销售公司又从中随机抽取了2辆作为奖品回馈消费者.求至少有一辆是舒适型轿车的概率.