(本小题满分10分)如图,在平面直角坐标系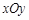 中,点
中,点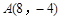 ,
,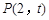
 在抛物线
在抛物线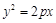
 上.
上.
(1)求 ,
, 的值;
的值;
(2)过点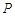 作
作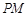 垂直于
垂直于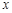 轴,
轴,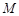 为垂足,直线
为垂足,直线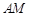 与抛物线的另一交点为
与抛物线的另一交点为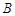 ,点
,点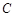 在直线
在直线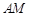 上.若
上.若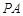 ,
,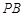 ,
, 的斜率分别为
的斜率分别为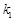 ,
, ,
,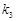 ,且
,且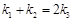 ,求点
,求点 的坐标.
的坐标.
将数列 按如图所示的规律排成一个三角形数表,并同时满足以下两个条件:①各行的第一
按如图所示的规律排成一个三角形数表,并同时满足以下两个条件:①各行的第一
个数 构成公差为
构成公差为 的等差数列;②从第二行起,每行各数按从左到右的顺序都构成公比为
的等差数列;②从第二行起,每行各数按从左到右的顺序都构成公比为 的等比数列.若
的等比数列.若 ,
, ,
, .
.
(1)求 的值;
的值;
(2)求第 行各数的和
行各数的和 .
.
某校为了解高一期末数学考试的情况,从高一的所有学生数学试卷中随机抽取 份试卷进行成绩分析,得到数学成绩频率分布直方图(如图所示),其中成绩在
份试卷进行成绩分析,得到数学成绩频率分布直方图(如图所示),其中成绩在 的学生人数为6.
的学生人数为6.
(1)估计所抽取的数学成绩的众数;
(2)用分层抽样的方法在成绩为 和
和 这两组中共抽取5个学生,并从这5个学生中任取2人进行点评,求分数在
这两组中共抽取5个学生,并从这5个学生中任取2人进行点评,求分数在 恰有1人的概率.
恰有1人的概率.
设函数 .
.
(1)求不等式 的解集
的解集 ;
;
(2)若存在实数 ,使得
,使得 成立,求实数
成立,求实数 的取值范围.
的取值范围.
已知在平面直角坐标系 中,圆
中,圆 的方程为
的方程为 .以原点
.以原点 为极点,以
为极点,以 轴正半轴为极轴,且与直角坐标系取相同的单位长度,建立极坐标系,直线
轴正半轴为极轴,且与直角坐标系取相同的单位长度,建立极坐标系,直线 的极坐标方程为
的极坐标方程为 .
.
(1)求直线 的直角坐标方程和圆
的直角坐标方程和圆 的参数方程;
的参数方程;
(2)求圆 上的点到直线
上的点到直线 的距离的最小值.
的距离的最小值.
若二阶矩阵 满足:
满足: .
.
(1)求二阶矩阵 ;
;
(2)若曲线 在矩阵
在矩阵 所对应的变换作用下得到曲线
所对应的变换作用下得到曲线 ,求曲线
,求曲线 的方程.
的方程.