如图,某市有一条东西走向的公路 ,现欲经过公路
,现欲经过公路 上的
上的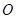 处铺设一条南北走向的公路
处铺设一条南北走向的公路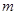 .在施工过程中发现在
.在施工过程中发现在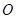 处的正北
处的正北 百米的
百米的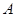 处有一汉代古迹.为了保护古迹,该市决定以
处有一汉代古迹.为了保护古迹,该市决定以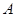 为圆心,
为圆心, 百米为半径设立一个圆形保护区.为了连通公路
百米为半径设立一个圆形保护区.为了连通公路 、
、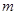 ,欲再新建一条公路
,欲再新建一条公路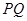 ,点
,点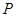 、
、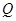 分别在公路
分别在公路 、
、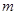 上,且要求
上,且要求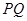 与圆
与圆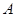 相切.
相切.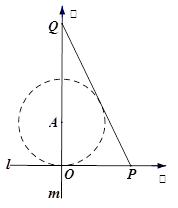
(1)当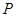 距
距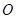 处
处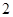 百米时,求
百米时,求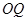 的长;
的长;
(2)当公路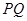 长最短时,求
长最短时,求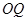 的长.
的长.
已知函数f(x)=(ax2+bx+c)ex且f(0)=1,f(1)=0.
(1)若f(x)在区间[0,1]上单调递减,求实数a的取值范围;
(2)当a=0时,是否存在实数m使不等式2f(x)+4xex≥mx+1≥-x2+4x+1对任意x∈R恒成立?若存在,求出m的值,若不存在,请说明理由.
已知抛物线C:y2=2px(p>0),M点的坐标为(12,8),N点在抛物线C上,且满足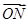 =
=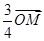 ,O为坐标原点.
,O为坐标原点.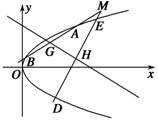
(1)求抛物线C的方程;
(2)以M点为起点的任意两条射线l1,l2的斜率乘积为1,并且l1与抛物线C交于A,B两点,l2与抛物线C交于D,E两点,线段AB,DE的中点分别为G,H两点.求证:直线GH过定点,并求出定点坐标.
如图,在矩形ABCD中,AB=2AD=2,O为CD的中点,沿AO将△AOD折起,使DB=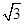 .
.
(1)求证:平面AOD⊥平面ABCO;
(2)求直线BC与平面ABD所成角的正弦值.
已知数列{an}满足a1=3,an+1=an+p·3n(n∈N*,p为常数),a1,a2+6,a3成等差数列.
(1)求p的值及数列{an}的通项公式;
(2)设数列{bn}满足bn=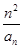 ,证明:bn≤
,证明:bn≤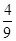 .
.
一个袋子装有大小形状完全相同的9个球,其中5个红球编号分别为1,2,3,4,5,4个白球编号分别为1,2,3,4,从袋中任意取出3个球.
(1)求取出的3个球编号都不相同的概率;
(2)记X为取出的3个球中编号的最小值,求X的分布列与数学期望.