(本题14分)已知函数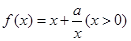 .
.
(1)若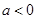 ,试用定义证明:
,试用定义证明: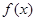 在
在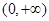 上单调递增;
上单调递增;
(2)若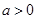 ,当
,当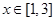 时不等式
时不等式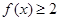 恒成立,求
恒成立,求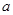 的取值范围.
的取值范围.
已知函数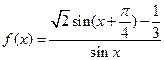 .
.
(Ⅰ)求函数 的定义域;
的定义域;
(Ⅱ)若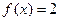 ,求
,求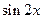 的值
的值
已知函数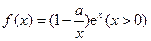 ,其中
,其中 为自然对数的底数.
为自然对数的底数.
(Ⅰ)当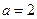 时,求曲线
时,求曲线 在
在 处的切线与坐标轴围成的面积;
处的切线与坐标轴围成的面积;
(Ⅱ)若函数 存在一个极大值点和一个极小值点,且极大值与极小值的积为
存在一个极大值点和一个极小值点,且极大值与极小值的积为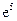 ,求
,求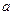 的值.
的值.
甲班有2名男乒乓球选手和3名女乒乓球选手,乙班有3名男乒乓球选手和1名女乒乓球选手,学校计划从甲乙两班各选2名选手参加体育交流活动.
(Ⅰ)求选出的4名选手均为男选手的概率.
(Ⅱ)记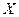 为选出的4名选手中女选手的人数,求
为选出的4名选手中女选手的人数,求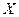 的分布列和期望.
的分布列和期望.
若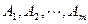 为集合
为集合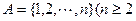 且
且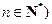 的子集,且满足两个条件:
的子集,且满足两个条件:
①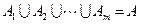 ;
;
②对任意的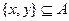 ,至少存在一个
,至少存在一个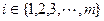 ,使
,使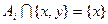 或
或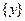 .
.
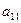 |
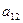 |
… |
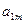 |
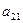 |
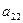 |
… |
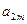 |
| … |
… |
… |
… |
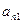 |
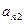 |
… |
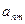 |
则称集合组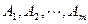 具有性质
具有性质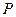 .
.
如图,作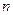 行
行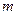 列数表,定义数表中的第
列数表,定义数表中的第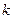 行第
行第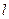 列的数为
列的数为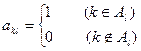 .
.
(Ⅰ)当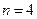 时,判断下列两个集合组是否具有性质
时,判断下列两个集合组是否具有性质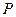 ,如果是请画出所对应的表格,如果不是请说明理由;
,如果是请画出所对应的表格,如果不是请说明理由;
集合组1: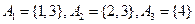 ;
;
集合组2: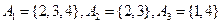 .
.
(Ⅱ)当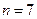 时,若集合组
时,若集合组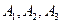 具有性质
具有性质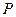 ,请先画出所对应的
,请先画出所对应的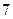 行3列的一个数表,再依此表格分别写出集合
行3列的一个数表,再依此表格分别写出集合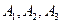 ;
;
(Ⅲ)当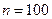 时,集合组
时,集合组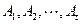 是具有性质
是具有性质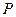 且所含集合个数最小的集合组,求
且所含集合个数最小的集合组,求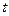 的值及
的值及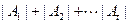 的最小值.(其中
的最小值.(其中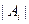 表示集合
表示集合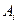 所含元素的个数)
所含元素的个数)
已知椭圆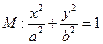
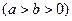 的离心率为
的离心率为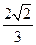 ,且椭圆上一点与椭圆的两个焦点构成的三角形周长为
,且椭圆上一点与椭圆的两个焦点构成的三角形周长为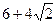 .
.
(Ⅰ)求椭圆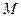 的方程;
的方程;
(Ⅱ)设直线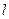 与椭圆
与椭圆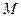 交于
交于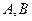 两点,且以
两点,且以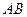 为直径的圆过椭圆的右顶点
为直径的圆过椭圆的右顶点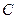 ,
,
求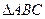 面积的最大值.
面积的最大值.