甲、乙、丙三所学校进行了一次八年级数学联合考试.老师们对其中的一道题进行了分析,把每个学生的解答情况归结为下列四种情况之一:A~概念错误;B~计算错误;C~解答基本正确,但不完整;D~解答完全正确.
各校出现这四类种情况的人数分别占本校八年级学生数的百分比如下表.
| |
A |
B |
C |
D |
| 甲校(%) |
6.25 |
12.75 |
44.75 |
36.25 |
| 乙校(%) |
3.4 |
14.6 |
24.4 |
57.6 |
| 丙校(%) |
13.3 |
31.7 |
17 |
38 |
各校八年级学生人数的扇形统计图如图.
已知甲校八年级有400名学生,根据以上信息,解答下列问题:
(1)求三校八年级学生总数;
(2)求三校解答完全正确的学生总数占三校八年级学生总数的百分比m(精确到0.01%);
(3)请你对表中三校的数据进行对比分析,给丙校八年级数学老师们提一个值得关注的问题,并说明理由.
(·温州卷 第24题 14分)如图,点A和动点P在直线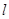 上,点P关于点A的对称点为Q,以AQ为边作Rt△ABQ,使∠BAQ=90°,AQ:AB=3:4,作△ABQ的外接圆O。点C在点P右侧,PC=4,过点C作直线
上,点P关于点A的对称点为Q,以AQ为边作Rt△ABQ,使∠BAQ=90°,AQ:AB=3:4,作△ABQ的外接圆O。点C在点P右侧,PC=4,过点C作直线 ⊥
⊥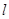 ,过点O作OD⊥
,过点O作OD⊥ 于点D,交AB右侧的圆弧于点E。在射线CD上取点F,使DF=
于点D,交AB右侧的圆弧于点E。在射线CD上取点F,使DF=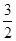 CD,以DE,DF为邻边作矩形DEGF,设AQ=
CD,以DE,DF为邻边作矩形DEGF,设AQ=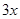

(1)用关于 的代数式表示BQ,DF;
的代数式表示BQ,DF;
(2)当点P在点A右侧时,若矩形DEGF的面积等于90,求AP的长;
(3)在点P的整个运动过程中,
①当AP为何值时,矩形DEGF是正方形?
②作直线BG交⊙O于另一点N,若BN的弦心距为1,求AP的长(直接写出答案)
(·温州卷 第23题 12分)如图,抛物线 交
交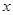 轴正半轴于点A,顶点为M,对称轴NB交
轴正半轴于点A,顶点为M,对称轴NB交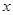 轴于点B,过点C(2,0)作射线CD交MB于点D(D在
轴于点B,过点C(2,0)作射线CD交MB于点D(D在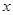 轴上方),OE∥CD交MB于点E,EF∥
轴上方),OE∥CD交MB于点E,EF∥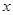 轴交CD于点F,作直线MF。
轴交CD于点F,作直线MF。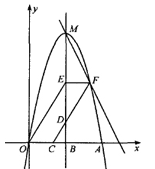
(1)求点A,M的坐标;
(2)当BD为何值时,点F恰好落在抛物线上?
(3)当BD=1时,①、求直线MF的解析式,并判断点A是否落在该直线上;
②、延长OE交FM于点G,取CF中点P,连结PG,△FPG,四边形DEGP,四边形OCDE的面积分别记为S1,S2,S3,则S1:S2:S3= .
(·台州市 第24题 14分)定义:如图1,点M,N把线段AB分割成AM,MN和BN,若以AM,MN,BN为边的三角形是一个直角三角形,则称点M,N是线段AB的勾股分割点
(1)已知点M,N是线段AB的勾股分割点,若AM=2,MN=3求BN的长;
(2)如图2,在△ABC中,FG是中位线,点D,E是线段BC的勾股分割点,且EC>DE≥BD,连接AD,AE分别交FG于点M,N,求证:点M,N是线段FG的勾股分割点
(3)已知点C是线段AB上的一定点,其位置如图3所示,请在BC上画一点D,使C,D是线段AB的勾股分割点(要求尺规作图,保留作图痕迹,画出一种情形即可)
(4)如图4,已知点M,N是线段AB的勾股分割点,MN>AM≥BN,△AMC,△MND和△NBM均是等边三角形,AE分别交CM,DM,DN于点F,G,H,若H是DN的中点,试探究 ,
, 和
和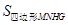 的数量关系,并说明理由
的数量关系,并说明理由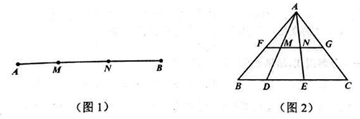

(·绍兴市 第24题 14分)
在平面直角坐标系中,O为原点,四边形OABC的顶点A在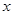 轴的正半轴上,OA=4,OC=2,点P,点Q分别是边BC,边AB上的点,连结AC,PQ,点B1是点B关于PQ的对称点。
轴的正半轴上,OA=4,OC=2,点P,点Q分别是边BC,边AB上的点,连结AC,PQ,点B1是点B关于PQ的对称点。
(1)若四边形OABC为矩形,如图1,
①求点B的坐标;
②若BQ:BP=1:2,且点B1落在OA上,求点B1的坐标;
(2)若四边形OABC为平行四边形,如图2,且OC⊥AC,过点B1作B1F∥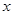 轴,与对角线AC、边OC分别交于点E、点F。若B1E: B1F=1:3,点B1的横坐标为
轴,与对角线AC、边OC分别交于点E、点F。若B1E: B1F=1:3,点B1的横坐标为 ,求点B1的纵坐标,并直接写出
,求点B1的纵坐标,并直接写出 的取值范围。
的取值范围。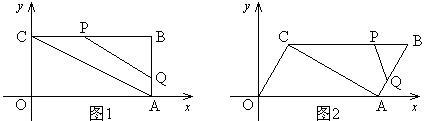
(·丽水市 第24题 12分)某乒乓球馆使用发球机进行辅助训练,出球口在桌面中线端点A处的正上方,假设每次发出的乒乓球的运动路线固定不变,且落在中线上,在乒乓球运行时,设乒乓球与端点A的水平距离为 (米),与桌面的高度为
(米),与桌面的高度为 (米),运行时间为
(米),运行时间为 (秒),经多次测试后,得到如下部分数据:
(秒),经多次测试后,得到如下部分数据:
 (秒) (秒) |
0 |
0.16 |
0.2 |
0.4 |
0.6 |
0.64 |
0.8 |
… |
 (米) (米) |
0 |
0.4 |
0.5 |
1 |
1.5 |
1.6 |
2 |
… |
 (米) (米) |
0.25 |
0.378 |
0.4 |
0.45 |
0.4 |
0.378 |
0.25 |
… |

(1)当 为何值时,乒乓球达到最大高度?
为何值时,乒乓球达到最大高度?
(2)乒乓球落在桌面时,与端点A的水平距离是多少?
(3)乒乓球落在桌面上弹起后, 与
与 满足
满足
①用含 的代数式表示
的代数式表示 ;
;
②球网高度为0.14米,球桌长(1.4×2)米,若球弹起后,恰好有唯一的击球点,可以将球沿直线扣杀到点A,求 的值。
的值。