为了有效地利用电力资源,电力部门推行分时用电.即在居民家中安装分时电表,每天6:00至22:00用电每千瓦时0.61元,每天22:00至次日6:00用电每千瓦时0.30元.原来不实行分时用电时,居民用电每千瓦时0.61元.某户居民为了解家庭的用电及电费情况,于去年9月随意记录了该月6天的用电情况,见下表(单位:千瓦时).
| 序 号 |
1 |
2 |
3 |
4 |
5 |
6 |
| 6:00至22:00用电量 |
4.5 |
4.4 |
4.6 |
4.6 |
4.3 |
4.6 |
| 22:00至次日6:00用电量 |
1.4 |
1.6 |
1.3 |
1.5 |
1.7 |
1.5 |
(1)如果该用户去年9月份(30天)每天的用电情况基本相同,根据表中数据,试估计该用户去年9月总用电量约为多少千瓦时.
(2)如果该用户今年3月份的分时电费为127.8元,而按照不实行分时用电的计费方法,其电费为146.4元,试问该用户今年3月份6:00至22:00与22:00至次日6:00两个时段的用电量各为多少千瓦时?(注:以上统计是从每个月的第一天6:00至下一个月的第一天6:00止)
如图,已知 与
与 都是等边三角形,点
都是等边三角形,点 在边
在边 上(不与
上(不与 、
、 重合),
重合), 与
与 相交于点
相交于点 .
.
(1)求证:
 ∽
∽ ;
;
(2)若 ,设
,设 ,
, ;
;
①求 关于
关于
 的函数解析式及定义域;
的函数解析式及定义域;
②当 为何值时,
为何值时, ?
?
已知抛物线 与
与 轴交于点
轴交于点 ,点
,点 是抛物线上的点,且满足
是抛物线上的点,且满足 ∥
∥ 轴,点
轴,点 是抛物线的顶点.
是抛物线的顶点.
(1)求抛物线的对称轴及 点坐标;
点坐标;
(2)若抛物线经过点 ,求抛物线的表达式;
,求抛物线的表达式;
(3)对(2)中的抛物线,点 在线段
在线段 上,若以点
上,若以点 、
、 、
、 为顶点的三角形与
为顶点的三角形与 相似,试求点
相似,试求点 的坐标.
的坐标.
如图,一块梯形木料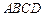 ,
,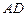 ∥
∥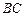 ,经测量知
,经测量知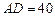 cm,
cm,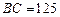 cm,
cm,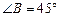 ,
,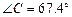 ,求梯形木料
,求梯形木料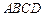 的高.
的高.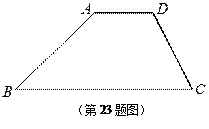
(备用数据 :sin 67.4° = ,cos 67.4° = ,tan 67.4° = )
:sin 67.4° = ,cos 67.4° = ,tan 67.4° = )
如图,已知在四边形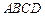 中,
中,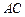 与
与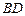 相交于点
相交于点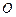 ,AB⊥AC,CD⊥BD.
,AB⊥AC,CD⊥BD.
(1)求证: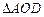 ∽
∽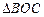 ;
;
(2)若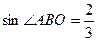 ,
,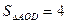 ,求
,求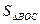 的值
的值
如图,已知在Rt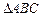 中,
中,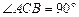 ,点
,点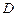 在
在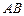 上,
上,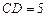 ,
,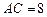 ,
, 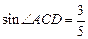 ,求
,求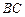 的长.
的长.