如图, 内接于 ,且 为 的直径, ,与 交于点 ,与过点 的 的切线交于点 .
(1)若 , ,求 的长.
(2)试判断 与 的数量关系,并说明理由.

从共享单车,共享汽车等共享出行到共享充电宝,共享雨伞等共享物品,各式各样的共享经济模式在各个领域迅速普及应用,越来越多的企业与个人成为参与者与受益者.根据国家信息中心发布的《中国分享经济发展报告2017》显示,2016年我国共享经济市场交易额约为34520亿元,比上年增长 ;超6亿人参与共享经济活动,比上年增加约1亿人.
如图是源于该报告中的中国共享经济重点领域市场规模统计图:

(1)请根据统计图解答下列问题:
①图中涉及的七个重点领域中,2016年交易额的中位数是 2038 亿元.
②请分别计算图中的“知识技能”和“资金”两个重点领域从2015年到2016年交易额的增长率(精确到 ,并就这两个重点领域中的一个分别从交易额和增长率两个方面,谈谈你的认识.
(2)小宇和小强分别对共享经济中的“共享出行”和“共享知识”最感兴趣,他们上网查阅了相关资料,顺便收集到四个共享经济领域的图标,并将其制成编号为 , , , 的四张卡片(除编号和内容外,其余完全相同)他们将这四张卡片背面朝上,洗匀放好,从中随机抽取一张(不放回),再从中随机抽取一张,请用列表或画树状图的方法求抽到的两张卡片恰好是“共享出行”和“共享知识”的概率(这四张卡片分别用它们的编号 , , , 表示)

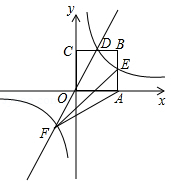
如图,在平面直角坐标系中,正方形 的顶点 与坐标原点重合,其边长为2,点 ,点 分别在 轴, 轴的正半轴上,函数 的图象与 交于点 ,函数 为常数, 的图象经过点 ,与 交于点 ,与函数 的图象在第三象限内交于点 ,连接 、 .
(1)求函数 的表达式,并直接写出 、 两点的坐标;
(2)求 的面积.
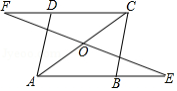
已知:如图,在 中,延长 至点 ,延长 至点 ,使得 .连接 ,与对角线 交于点 .
求证: .
综合与探究
如图,在平面直角坐标系中,已知抛物线 与 轴交于 , 两点,与 轴交于点 ,直线 经过坐标原点 ,与抛物线的一个交点为 ,与抛物线的对称轴交于点 ,连接 ,已知点 , 的坐标分别为 , .
(1)求抛物线的函数表达式,并分别求出点 和点 的坐标;
(2)试探究抛物线上是否存在点 ,使 ?若存在,请直接写出点 的坐标;若不存在,请说明理由;
(3)若点 是 轴负半轴上的一个动点,设其坐标为 ,直线 与直线 交于点 ,试探究:当 为何值时, 是等腰三角形.
