如图,在△ABC中,AB=AC,以AB为直径作半圆⊙0,交BC于点D,连接AD,过点D作DE⊥AC,垂足为点E,交AB的延长线于点F.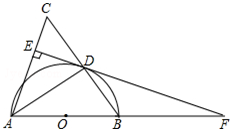
(1)求证:EF是⊙0的切线;
(2)如果⊙0的半径为9,sin∠ADE=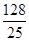 ,求AE的长.
,求AE的长.
(本小题满分9分)如图,已知直线l1∥l2,线段AB在直线l1上,BC垂直于l1交l2于点C,且AB=BC,P是线段BC上异于两端点的一点,过点P的直线分别交l2、 l1于点D、E(点A、E位于点B的两侧),满足BP=BE,连结AP、CE.
(1)求证:△ABP≌△CBE;
(2)连结AD、BD,BD与AP相交于点F,如图,
①当 时,求证:AP⊥BD;
时,求证:AP⊥BD;
② (n>1)时,设△PAD的面积为S1,△PCE的面积为S2,求
(n>1)时,设△PAD的面积为S1,△PCE的面积为S2,求 的值.
的值.
(本小题满分9分)如图,点A(3,2)和点M(m,n)都在反比例函数 的图像上.
的图像上.
(1)求k的值,并求当m=4时,直线AM的解析式;
(2)过点M作MP⊥x轴,垂足为P,过点A作AB⊥y轴,垂足为B,直线AM交x轴于点Q,试说明四边形ABPQ是平行四边形.
(3)在(2)的条件下,四边形ABPQ能否是菱形?若能,请求出m的值,若不能,请说明理由.
(本小题满分8分)第一次模拟考试后,数学科陈老师把一班的数学成绩制成如下图的统计图,并给了几个信息:① 前两组的频率和是0.14;② 第一组的频率是0.02;③ 自左至右第二、三、四组的频数比为3︰9︰8.然后布置学生(也请你一起)结合统计图完成下列问题:
(1)全班学生是多少人?
(2)成绩不少于90分为优秀,那么全班成绩的优秀率是多少?
(3)若不少于100分可以得到A+等级,则小明得到A+的概率是多少?
(本小题满分8分)如图,某数学兴趣小组想测量一棵树CD的高度,他们先在点A处测得树顶C的仰角为30°,然后沿AD方向前行10m,到达B点,在B处测得树顶C的仰角高度为60°(A、B、D三点在同一直线上).请你根据他们测量数据计算这棵树CD的高度(结果精确到0.1m).(参考数据: ≈1.414,
≈1.414, ≈1.732)
≈1.732)
(本小题满分7分)完成下列各题:
(1)如图,△ABC和△ADE中,∠BAC=∠DAE,AB=AE,AC=AD,连接BD,CE,求证:△ABD≌△AEC.
(2)如图,AB是⊙O的弦,∠OAB=20°,求弦AB所对的圆周角的度数.