如图，抛物线yax2bxc经过点A（﹣3，0），B（1．0）-优题课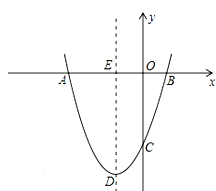

如图，抛物线y=ax²+bx+c经过点A（﹣3，0），B（1．0），C（0，﹣3）．

（1）求抛物线的解析式；
（2）若点P为第三象限内抛物线上的一点，设△PAC的面积为S，求S的最大值并求出此时点P的坐标；
（3）设抛物线的顶点为D，DE⊥x轴于点E，在y轴上是否存在点M，使得△ADM是直角三角形？若存在，请直接写出点M的坐标；若不存在，请说明理由．

科目数学题型解答题难度中等

知识点：二次函数在给定区间上的最值

某商场经营一种海产品，进价是每千克20元，根据市场调查发现，每日的销售量 $y$ （千克）与售价 $x$ （元 $/$ 千克）是一次函数关系，如图所示：

（1）求 $y$ 与 $x$ 的函数关系式（不求自变量取值范围）；

（2）某日该商场出售这种海产品获得了21000元的利润，该海产品的售价是多少？

（3）若某日该商场这种海产品的销售量不少于650千克，该商场销售这种海产品获得的最大利润是多少？

如图， $ΔABC$ 内接于 $⊙ O$ ， $BC$ 是 $⊙ O$ 的直径，点 $A$ 是 $⊙ O$ 上的定点， $AD$ 平分 $∠ BAC$ 交 $⊙ O$ 于点 $D$ ， $DG / / BC$ ，交 $AC$ 延长线于点 $G$ ．

（1）求证： $DG$ 与 $⊙ O$ 相切；

（2）作 $BE ⊥ AD$ 于点 $E$ ， $CF ⊥ AD$ 于点 $F$ ，试判断线段 $BE$ 、 $CF$ 、 $EF$ 三者之间的数量关系，并证明你的结论（不用尺规作图的方法补全图形）．

如图，四边形 $ABCD$ 是矩形 $(AB < BC)$ ，要在矩形 $ABCD$ 内作一个以 $AB$ 为边的正方形 $ABEF$ ，某位同学的作法如下：

①作 $∠ ABC$ 的平分线 $BM$ ． $BM$ 交 $AD$ 于点 $F$ ；

②以点 $B$ 为圆心， $BA$ 长为半径画弧，交 $BC$ 于点 $E$ ，连接 $EF$ ．

（1）求证：四边形 $ABEF$ 是正方形；

（2）若 $AB = 5$ ，求图中阴影部分的面积．

在阳光大课间活动中，某校开展了立定跳远、实心球、长跑等体育活动，为了了解九年级一班学生的立定跳远成绩的情况，对全班学生的立定跳远测试成绩进行统计，并绘制了以下不完整的频数分布直方图和扇形图，根据图中信息解答下列问题．

（1）求九年级一班学生总人数，并补全频数分布直方图（标注频数）；

（2）求 $2.05 ⩽ a ⩽ 2.25$ 成绩段在扇形统计图中对应的圆心角度数；

（3）直接写出九年级一班学生立定跳远成绩的中位数所在的成绩段；

（4）九年级一班在 $2.05 ⩽ a ⩽ 2.45$ 成绩段中有男生3人，女生2人，现要从这5人中随机抽取2人参加学校运动会，请用列表法或画树状图的方法求出恰好抽到一男一女的概率．

如图，一棵与地面垂直的笔直大树 $AB$ ，在点 $C$ 被大风折断后， $AC$ 部分倒下，树的顶点 $A$ 与斜坡 $DF$ 上的点 $G$ 重合 $(BC$ ， $CG$ 都保持笔直），经测量 $DG = 2 m$ ， $BD = 3 m$ ， $∠ EDF = 30 °$ ， $∠ BCG = 60 °$ ，求 $CG$ 的长． $(\sqrt{3} \approx 1.73$ ，精确到 $0.1 m)$