(本小题满分13分)已知函数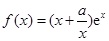 ,
, .
.
(Ⅰ)当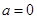 时,求曲线
时,求曲线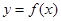 在点
在点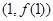 处的切线方程;
处的切线方程;
(Ⅱ)当 时,求证:
时,求证: 在
在 上为增函数;
上为增函数;
(Ⅲ)若 在区间
在区间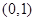 上有且只有一个极值点,求
上有且只有一个极值点,求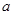 的取值范围.
的取值范围.
已知动点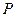 到定点
到定点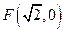 的距离与点
的距离与点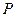 到定直线
到定直线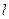 :
: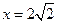 的距离之比为
的距离之比为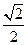 .
.
(1)求动点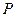 的轨迹
的轨迹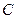 的方程;
的方程;
(2)设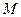 、
、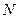 是直线
是直线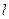 上的两个点,点
上的两个点,点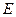 与点
与点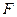 关于原点
关于原点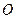 对称,若
对称,若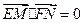 ,求
,求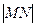 的最小值.
的最小值.
已知直线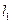 :
: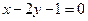 ,直线
,直线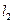 :
: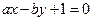 ,其中
,其中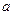 ,
,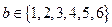 .
.
(1)求直线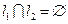 的概率;
的概率;
(2)求直线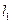 与
与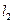 的交点位于第一象限的概率.
的交点位于第一象限的概率.
已知函数 (
( )的最小正周期为
)的最小正周期为 .
.
(Ⅰ)求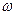 的值;
的值;
(Ⅱ)求函数 在区间
在区间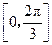 上的取值范围.
上的取值范围.
新课标要求学生数学模块学分认定由模块成绩决定,模块成绩由模块考试成绩和平时成绩构成,各占50%,若模块成绩大于或等于60分,获得2学分,否则不能获得学分(为0分),设计一算法,通过考试成绩和平时成绩计算学分,并画出程序框图。
已知直线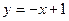 与椭圆
与椭圆 相交于A、B两点,且线段AB的中点,在直线
相交于A、B两点,且线段AB的中点,在直线 上.(1)求此椭圆的离心率;(2)若椭圆的右焦点关于直线
上.(1)求此椭圆的离心率;(2)若椭圆的右焦点关于直线 的对称点的在圆
的对称点的在圆 上,求此椭圆的方程.
上,求此椭圆的方程.