已知数列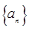 满足:
满足: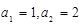 ,且
,且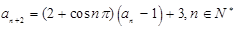 。
。
(1)求通项公式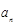 ;
;
(2)求数列的前n项的和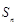
已知函数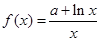 在点
在点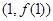 处的切线与x轴平行.
处的切线与x轴平行.
(1)求实数a的值及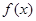 的极值;
的极值;
(2)是否存在区间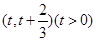 ,使函数
,使函数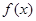 在此区间上存在极值和零点?若存在,求实数t的取值范围,若不存在,请说明理由;
在此区间上存在极值和零点?若存在,求实数t的取值范围,若不存在,请说明理由;
(3)如果对任意的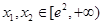 ,有
,有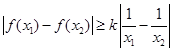 ,求实数k的取值范围.
,求实数k的取值范围.
已知抛物线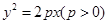 的焦点为F,点P是抛物线上的一点,且其纵坐标为4,
的焦点为F,点P是抛物线上的一点,且其纵坐标为4,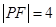 .
.
(1)求抛物线的方程;
(2)设点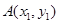 ,
, (
(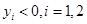 )是抛物线上的两点,∠APB的角平分线与x轴垂直,求△PAB的面积最大时直线AB的方程.
)是抛物线上的两点,∠APB的角平分线与x轴垂直,求△PAB的面积最大时直线AB的方程.
如图,已知AB⊥平面ACD,DE∥AB,△ACD是正三角形,AD=DE=2AB,且F是CD的中点。
(1)求证:AF∥平面BCE;
(2)求证:平面BCE⊥平面CDE;
(3)求平面BCE与平面ACD所成锐二面角的大小.
已知函数 .
.
(1)求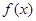 的单调递增区间;
的单调递增区间;
(2)在△ABC中,三内角A,B,C的对边分别为a,b,c,已知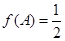 ,b,a,c成等差数列,且
,b,a,c成等差数列,且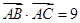 ,求a的值.
,求a的值.
已知数列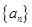 的前n项和为
的前n项和为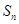 ,
,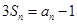
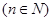 .
.
(1)求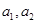 ;
;
(2)求证:数列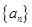 是等比数列;
是等比数列;
(3)求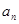 .
.