生产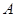
，
两种元件，其质量按测试指标划分为：指标大于或等于82为正品，小于82为次品，现随机抽取这两种元件各100件进行检测，检测结果统计如下：
| 测试指标 |
 |
 |
 |
 |
 |
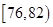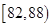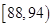| 元件 |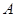
8 |
12 |
40 |
32 |
8 |
| 元件 |
7 |
18 |
40 |
29 |
6 |
（Ⅰ）试分别估计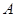元件、元件为正品的概率；
（Ⅱ）生产一件元件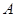，若是正品可盈利50元，若是次品则亏损10元；生产一件元件，若是正品可盈利100元，若是次品则亏损20元，在（Ⅰ）的前提下
（i）求生产5件元件所获得的利润不少于300元的概率；
（ii）记
为生产1件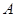元件和1件元件所得的总利润，求随机变量的分布列和期望．
5｝，B=｛x︱x2+x
2｝，求A
(
uB).