（本小题满分10分）选修4-4：坐标系与参数方程
已知椭圆C：
，直线
（t为参数）．
（Ⅰ）写出椭圆C的参数方程及直线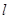
的普通方程；
（Ⅱ）设
，若椭圆C上的点P满足到点A的距离与其到直线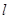的距离相等，求点P的坐标．
(本题满分14分)．如图所示，四棱锥P－ABCD的底面积ABCD是边长为1的菱形，
∠BCD＝60°，E是CD的中点，PA⊥底面积ABCD，PA＝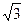
.
(Ⅰ)证明：平面PBE⊥平面PAB；
(Ⅱ) 过PC中点F作FH//平面PBD, FH交平面ABCD于H点，判定H点位于平面ABCD的那个具体位置？（无须证明）
（Ⅲ）求二面角A－BE－P的大小.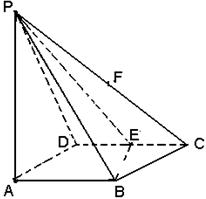 
(本题满分14分)．如图,圆锥的轴截面SAB为等腰直角三角形，Q为底面圆周上的一点，如果QB的中点为C，OH⊥SC，垂足为H。
求证：BQ⊥平面SOC，
求证：OH⊥平面SBQ；设
,
,求此圆锥的体积。
(本题满分14分)．如图，在棱长为4的正方体ABCD-A1B1C1D1中，E是D1C1上的一点且EC1=3D1 E，
(1) 求直线BE与平面ABCD所成角的正切值；
(2)求异面直线BE与CD所成角的余弦值.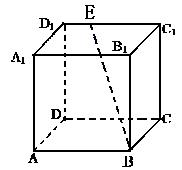 
(本题满分12分)．如图，在三棱柱ABC－
中，点E，D分别是
与BC的中点．
求证：平面
EB//平面AD
．
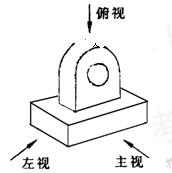
(本题满分12分)．画出右边水平放置的几何体的三视图.