如图,在四棱锥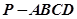 中,
中,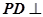 平面
平面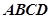 ,底面
,底面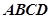 是菱形,
是菱形,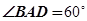 ,
,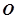 为
为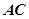 与
与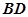 的交点,
的交点,  为
为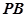 上任意一点.
上任意一点.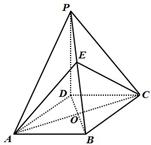
(Ⅰ)证明:平面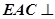 平面
平面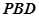 ;
;
(Ⅱ)若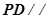 平面
平面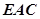 ,并且二面角
,并且二面角 的大小为
的大小为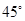 ,求
,求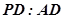 的值.
的值.
设- ≤x≤
≤x≤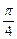 ,求函数y=log2(1+sinx)+log2(1-sinx)的最大值和最小值.
,求函数y=log2(1+sinx)+log2(1-sinx)的最大值和最小值.
有一块半径为R,中心角为45°的扇形铁皮材料,为了获取面积最大的矩形铁皮,工人师傅常让矩形的一边在扇形的半径上,然后作其最大内接矩形,试问: 工人师傅是怎样选择矩形的四点的?并求出最大面积值.
用一块长为a,宽为b(a>b)的矩形木板,在二面角为α的墙角处围出一个直三棱柱的谷仓,试问应怎样围才能使谷仓的容积最大?并求出谷仓容积的最大值.
设二次函数f(x)=x2+bx+c(b,c∈R),已知不论α、β为何实数恒有f(sinα)≥0和f(2+cosβ)≤0。
(1)求证: b+c=-1;
(2)求证c≥3;
(3)若函数f(sinα)的最大值为8,求b,c的值.
已知点的序列An(xn,0),n∈N,其中x1=0,x2=a(a>0),A3是线段A1A2的中点,A4是线段A2A3的中点,…,An是线段An-2An-1的中点,….
(1)写出xn与xn-1、xn-2之间关系式(n≥3);
(2)设an=xn+1-xn,计算a1,a2,a3,由此推测数列{an}的通项公式,并加以证明;
(3)求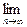 xn
xn