(本小题满分16分)在距A城市45千米的B地发现金属矿,过A有一直线铁路AD.欲运物资于A,B之间,拟在铁路线AD间的某一点C处筑一公路到B.现测得 千米,
千米, (如图).已知公路运费是铁路运费的2倍,设铁路运费为每千米1个单位,总运费为
(如图).已知公路运费是铁路运费的2倍,设铁路运费为每千米1个单位,总运费为 .为了求总运费
.为了求总运费 的最小值,现提供两种方案:方案一:设
的最小值,现提供两种方案:方案一:设 千米;方案二设
千米;方案二设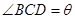 .
.
(1)试将 分别表示为
分别表示为 、
、 的函数关系式
的函数关系式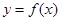 、
、 ;
;
(2)请选择一种方案,求出总运费 的最小值,并指出C点的位置.
的最小值,并指出C点的位置.
椭圆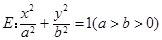 与双曲线
与双曲线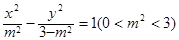 有公共的焦点,过椭圆E的右顶点作任意直线l,设直线l交抛物线
有公共的焦点,过椭圆E的右顶点作任意直线l,设直线l交抛物线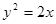 于M、N两点,且
于M、N两点,且 .
.
(1)求椭圆E的方程;
(2)设P是椭圆E上第一象限内的点,点P关于原点O的对称点为A、关于x轴的对称点为Q,线段PQ与x轴相交于点C,点D为CQ的中点,若直线AD与椭圆E的另一个交点为B,试判断直线PA,PB是否相互垂直?并证明你的结论.
已知函数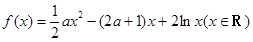 .
.
(1)若曲线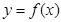 在x=l和x=3处的切线互相平行,求a的值及函数
在x=l和x=3处的切线互相平行,求a的值及函数 的单调区间;
的单调区间;
(2)设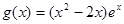 ,若对任意
,若对任意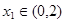 ,均存在
,均存在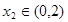 ,使得
,使得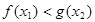 ,求实数a的取值范围.
,求实数a的取值范围.
近日,国家经贸委发出了关于深入开展增产节约运动,大力增产市场适销对路产品的通知,并发布了当前国内市场185种适销工业品和42种滞销产品的参考目录.为此,一公司举行某产品的促销活动,经测算该产品的销售量P万件(生产量与销售量相等)与促销费用x万元满足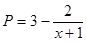 (其中
(其中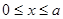 ,a为正常数).已知生产该产品还需投入成本10+2P万元(不含促销费用),产品的销售价格定为
,a为正常数).已知生产该产品还需投入成本10+2P万元(不含促销费用),产品的销售价格定为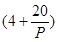 元/件.
元/件.
(1)将该产品的利润y万元表示为促销费用x万元的函数;
(2)促销费用投入多少万元时,厂家的利润最大.
已知数列 的前n项和为Sn,对一切正整数n,点
的前n项和为Sn,对一切正整数n,点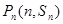 在函数
在函数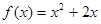 的图像上,且过点
的图像上,且过点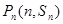 的切线的斜率为kn.
的切线的斜率为kn.
(1)求数列 的通项公式;
的通项公式;
(2)若 ,求数列
,求数列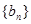 的前n项和Tn.
的前n项和Tn.
如图,菱形ABCD中, ,
, 平面ABCD,
平面ABCD, 平面ABCD,
平面ABCD,

(1)求证: 平面BDE;
平面BDE;
(2)求锐二面角 的大小.
的大小.