（本题满分10分) 选修4—1：几何问题选讲
如图，已知AB是⊙O的直径，弦CD与AB垂直，垂足为M，E是CD延长线上的一点，且AB=10，CD=8，3DE=4OM，过F点作⊙O的切线EF，BF交CD于G
（Ⅰ）求EG的长；
（Ⅱ）连接FD，判断FD与AB是否平行，为什么？
设命题p：f(x)＝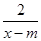
在区间(1，＋∞)上是减函数；命题q：x1，x2是方程x2－ax－2＝0的两个实根，且不等式m2＋5m－3≥|x1－x2|对任意的实数a∈[－1,1]恒成立．若p∧q为真，试求实数m的取值范围．
已知向量a＝
，b＝
，且x∈
.
(1)求a·b及|a＋b|；
(2)若f(x)＝a·b－2λ|a＋b|的最小值为－
，求正实数λ的值．
若复数z1与z2在复平面上所对应的点关于y轴对称，且z1(3－i)＝z2(1＋3i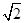)，|z1|＝
，求z1.
A，B分别是单位圆与x轴、y轴正半轴的交点，点P在单位圆上，∠AOP＝θ(0<θ<π)，C点坐标为(－2,0)，平行四边形OAQP的面积为S.
(1)求
·
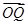＋S的最大值；
(2)若CB∥OP，求sin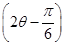
的值．
已知△ABC的内角A，B，C所对的边分别是a，b，c，设向量m＝(a，b)，n＝(sin B，sin A)，p＝(b－2，a－2)．
(1)若m∥n，求证：△ABC为等腰三角形；
(2)若m⊥p，边长c＝2，C＝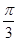
，求△ABC的面积．