已知椭圆 的中心在坐标原点,焦点在
的中心在坐标原点,焦点在 轴上,离心率为
轴上,离心率为 ,它的一个顶点恰好是抛物线
,它的一个顶点恰好是抛物线 的焦点.
的焦点.
(Ⅰ)求椭圆 的标准方程;
的标准方程;
(Ⅱ)若 ,
, 是椭圆
是椭圆 上关
上关 轴对称的任意两点,设点
轴对称的任意两点,设点 ,连接
,连接 交椭圆
交椭圆 于另一点
于另一点 ,求证:直线
,求证:直线 与
与 轴相交于定点
轴相交于定点 ;
;
(Ⅲ)设 为坐标原点,在(Ⅱ)的条件下,过点
为坐标原点,在(Ⅱ)的条件下,过点 的直线交椭圆
的直线交椭圆 于
于 ,
, 两点,求
两点,求 的取值范围.
的取值范围.
(本小题满分12分)某高校在2012年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组:第1组[160,165),第2组[165,170),第3组[170,175),第4组[175,180),第5组[180,185)得到的频率分布直方图如图所示。
(Ⅰ)求第3、4、5组的频率;
(Ⅱ)为了能选拔出最优秀的学生,该校决定在笔试成绩高的第3、4、5组中用分层抽样抽取6名学生进入第二轮面试,求第3、4、5组每组各抽取多少名学生进入第二轮面试?
(Ⅲ)在(Ⅱ)的前提下,学校决定在这6名学生中随机抽取2名学生接受甲考官的面试,求:第4组至少有一名学生被甲考官面试的概率?
(本小题满分12分) 若函数 的图象与直线
的图象与直线 相切,相邻切点之
相切,相邻切点之
间的距离为 。
。
(Ⅰ)求 和
和 的值;
的值;
(Ⅱ)若点 是
是 图象的对称中心,且
图象的对称中心,且 ,求点
,求点 的坐标。
的坐标。
(13分)一个同心圆形花坛,分为两部分,中间小圆部分种植绿色灌木,周围的圆环分为n(n≥3,n∈N)等份,种植红、黄、蓝三色不同的花,要求相邻两部分种植不同颜色的花.
⑴ 如图1,圆环分成的3等份为a1,a2,a3,有多少不同的种植方法?
如图2,圆环分成的4等份为a1,a2,a3,a4,有多少不同的种植方法?
⑵ 如图3,圆环分成的n等份为a1,a2,a3,……,an,有多少不同的种植方法?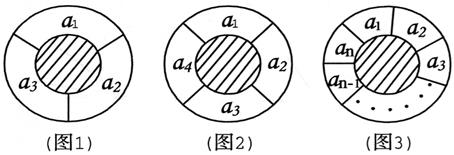
(12分) 已知数列 (n为正整数)是首项是a1,公比为q的等比数列.
(n为正整数)是首项是a1,公比为q的等比数列.
(1)求和: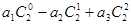 ,
,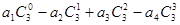
(2)由(1)的结果归纳概括出关于正整数n的一个结论,并加以证明.
(13分) 已知 的展开式中前三项的系数成等差数列.
的展开式中前三项的系数成等差数列.
(1)求n的值;
(2)求展开式中系数最大的项.