(本小题满分10分)选修4-1:几何证明选讲
如图,已知 是⊙
是⊙ 的直径,
的直径, 是⊙
是⊙ 的弦,
的弦,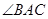 的平分线
的平分线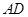 交⊙
交⊙ 于
于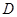 ,过点
,过点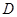 作
作 交
交 的延长线于点
的延长线于点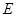 ,
,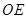 交
交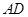 于点
于点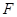 .若
.若 .
.
(Ⅰ)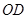 ∥
∥ ;
;
(Ⅱ)求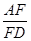 的值.
的值.
(本小题满分12分)
数列 的各项均为正数,
的各项均为正数,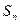 为其前
为其前 项和,对于任意
项和,对于任意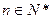 ,总有
,总有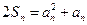 .
.
(1) 求数列 的通项公式;
的通项公式;
(2) 设正数数列 满足
满足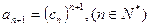 ,求数列
,求数列 中的最大项;
中的最大项;
已知数列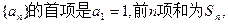

(1)设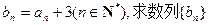 的通项公式;
的通项公式;
(2)设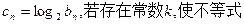
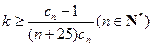 恒成立,求k的最小值。
恒成立,求k的最小值。
已知函数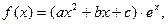 其中e为自然对数的底数,a,b,c为常数,若函数
其中e为自然对数的底数,a,b,c为常数,若函数 且
且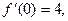
(1)求实数b,c的值;
(2)若函数 在区间[1,2]上是增函数,求实数a的取值范围。
在区间[1,2]上是增函数,求实数a的取值范围。
(本小题共12分)
如图,在正三棱柱ABC—A1B1C1中,点D是棱AB的中点,BC=1,AA1=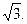
(1)求证:BC1//平面A1DC;
(2)求二面角D—A1C—A的大小
在△ABC中,a,b,c分别为角A,B,C所对的三边,
(1) 求角A;
(2) 若BC=2 ,角B等于x,周长为y,求函数
,角B等于x,周长为y,求函数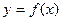 的取值范围.
的取值范围.