已知,如图1, 中,
中, ,
, 是平面内不与
是平面内不与 、
、 、
、 重合的任意一点,
重合的任意一点, ,
, .
.
(1)求证: ≌
≌ ;
;
(2)如图2,当点 是
是 的外接圆圆心时,请判断四边形
的外接圆圆心时,请判断四边形 的形状,并证明你的结论.
的形状,并证明你的结论.
解方程: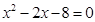
点P在图形M上, 点Q在图形N上,记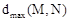 为线段PQ长度的最大值,
为线段PQ长度的最大值,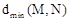 为线段PQ长度的最小值,图形M,N的平均距离
为线段PQ长度的最小值,图形M,N的平均距离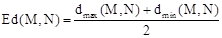 .
.
(1)在平面直角坐标系 中,⊙O是以O为圆心,2的半径的圆,且A
中,⊙O是以O为圆心,2的半径的圆,且A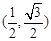 ,B
,B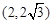 ,求
,求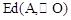 及
及 ;(直接写出答案即可)
;(直接写出答案即可)
(2)半径为1的⊙C的圆心C与坐标原点O重合,直线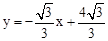 与
与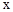 轴交于点D,与
轴交于点D,与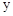 轴交于点F,记线段DF为图形G,求
轴交于点F,记线段DF为图形G,求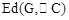 ;
;
(3)在(2)的条件下,如果⊙C的圆心C从原点沿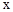 轴向右移动,⊙C的半径不变,且
轴向右移动,⊙C的半径不变,且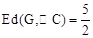 ,求圆心C的横坐标.
,求圆心C的横坐标.
在△ABC中,AB=AC,∠BAC<60°,把线段BC绕点B逆时针旋转60°至BP;如图所示位置有∠ABQ=60°,∠BCQ=150°.
(1)若∠BAC=30°,则∠ABP=度;若∠BAC=α,则∠ABP=(用α表示);
(2)求证:△ABQ为等边三角形;
(3)四边形CBPQ的面积为1,求△ABC的面积.
已知关于 的一元二次方程
的一元二次方程 .
.
(1)若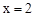 是该方程的一个根,求
是该方程的一个根,求 的值;
的值;
(2)无论 取任何值,该方程的根不可能为
取任何值,该方程的根不可能为 ,写出
,写出 的值,并证明;
的值,并证明;
(3)若 为正整数,且该方程存在正整数解,求所有正整数
为正整数,且该方程存在正整数解,求所有正整数 的值.
的值.
如图,已知点C、D在以O为圆心,AB为直径的半圆上,且OC⊥BD于点M,CF⊥AB于点F交BD于点E,BD=8,CM=2.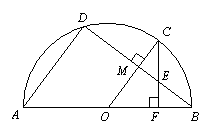
(1)求⊙O的半径;
(2)求证:CE=BE.