(本小题满分13分)
某公司经销农产品业务,以3万元/吨的价格向农户收购农产品后,以甲、乙两种方式进行销售,甲方式包装后直接销售;乙方式深加工后再销售.甲方式农产品的包装成本为1万元/吨,根据市场调查,它每吨平均销售价格y(单位:万元)与销售量m(单位:吨)之间的函数关系为y = -m+14(2≤m≤8);乙方式农产品深加工等(不含进价)总费用S(单位:万元)与销售量n(单位:吨)之间的函数关系是S=3n+12,平均销售价格为9万元/吨.
参考公式:抛物线y=ax2+bx+c(a≠0)的顶点坐标是(-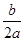 ,
,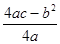 )
)
(1)该公司收购了20吨农产品,其中甲方式销售农产品x吨,其余农产品用乙方式销售,经销这20吨农产品所获得的毛利润为w万元(毛利润=销售总收入-经营总成本).
①直接写出:甲方式购买和包装x吨农产品所需资金为_________万元;乙方式购买和加工其余农产品所需资金为_________万元;
②求出w关于x的函数关系式;
③若农产品全部销售该公司共获得了48万元毛利润,求x的值;
④若农产品全部售出,该公司的最小利润是多少.
(2)该公司现有流动资金132万元,若将现有流动资金全部用于经销农产品,
①其中甲方式经销农产品x吨,则总经销量p为__________吨(用含x的代数式表示);
②当x为何值时,使公司获得最大毛利润,并求出最大毛利润.
已知直线l上有一点O,点A、B同时从O出发,在直线l上分别向左、向右作匀速运动,且A、B的速度比为1:2,设运动时间为ts.
(1)当t=2s时,AB=12cm.此时,
①在直线l上画出A、B两点运动2秒时的位置,并回答点A运动的速度是 cm/s; 点B运动的速度是 cm/s.
②若点P为直线l上一点,且PA﹣PB=OP,求 的值;
的值;
(2)在(1)的条件下,若A、B同时按原速向左运动,再经过几秒,OA=2OB.
为庆祝第29届北京奥运圣火在泉州站传递,甲、乙两校联合准备文艺汇演.甲、乙两校共92人(其中甲校人数多于乙校人数,且甲校人数不够90人)准备统一购买服装(一人买一套)参加演出,下面是服装厂给出的演出服装的价格表:
| 购买服装的套数 |
1套至45套 |
46套至90套 |
91套及以上 |
| 每套服装的价格 |
60元 |
50元 |
40元 |
如果两所学校分别单独购买服装,一共应付5000元.
(1)如果甲、乙两校联合起来购买服装,那么比各自购买服装共可以节省多少钱?
(2)甲、乙两校各有多少学生准备参加演出?
(3)如果甲校有9名同学抽调去参加迎奥运书法比赛不能参加演出,那么你有几种购买方案,通过比较,你该如何购买服装才能最省钱?
如图,已知∠COB=2∠AOC,OD平分∠AOB,且∠COD=23°,求∠AOB的度数.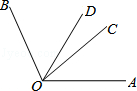
在图的正方形网格中有一个三角形OAB,请你在网格中分别按下列要求画出图形
①画出△OAB向左平移3个单位后的三角形;
②画出△OAB绕点O旋转180°后的三角形;
③画出△OAB沿y轴翻折后的图形.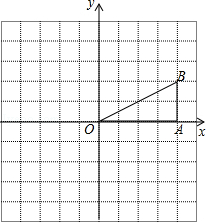
(1)由大小相同的小立方块搭成的几何体如下图,请在下图的方格中画出该几何体的俯视图和左视图.
(2)用小立方体搭一几何体,使得它的俯视图和左视图与你在上图方格中所画的图一致,则这样的几何体最少要 个小立方块,最多要 个小立方块.