(本小题满分12分) 设函数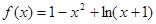
(1)求函数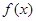 的单调区间;
的单调区间;
(2)若不等式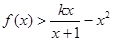 (
(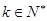 )在
)在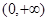 上恒成立,求
上恒成立,求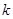 的最大值.
的最大值.
(本小题满分14分)已知递增数列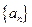 满足:
满足: ,
,
 ,且
,且 、
、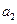 、
、 成等比数列。(I)求数列
成等比数列。(I)求数列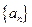 的通项公式
的通项公式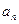 ;(II)若数列
;(II)若数列 满足:
满足: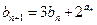
 ,且
,且 。①证明数列
。①证明数列 是等比数列,并求数列
是等比数列,并求数列 的通项公式
的通项公式 ;②设
;②设 ,数列
,数列 前
前 项和为
项和为 ,
,
 ,
, 。当
。当 时,试比较A与B的大小。
时,试比较A与B的大小。
(本小题满分12分)已知函数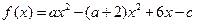 (
( 为实常数)(Ⅰ)若函数
为实常数)(Ⅰ)若函数 为奇函数,求此函数的单调区间;(Ⅱ)记
为奇函数,求此函数的单调区间;(Ⅱ)记 ,当
,当 ,试讨论函数
,试讨论函数 的图象与函数
的图象与函数 的图象的交点个数.
的图象的交点个数.
(本小题满分12分)已知函数
(I)求 的值;(II)解不等式:
的值;(II)解不等式:
(本小题满分12分)某公司是否对某一项目投资,由甲、乙、丙三位决策人投票决定.他们三人都有“同意”、“中立”、“反对”三类票各一张.投票时,每人必须且只能投一张票,每人投三类票中的任何一类票的概率都为 ,他们的投票相互没有影响.规定:若投票结果中至少有两张“同意”票,则决定对该项目投资;否则,放弃对该项目投资.(Ⅰ)求此公司决定对该项目投资的概率(Ⅱ)求此公司放弃对该项目投资且投票结果中最多有一张“中立”票的概率。
,他们的投票相互没有影响.规定:若投票结果中至少有两张“同意”票,则决定对该项目投资;否则,放弃对该项目投资.(Ⅰ)求此公司决定对该项目投资的概率(Ⅱ)求此公司放弃对该项目投资且投票结果中最多有一张“中立”票的概率。
(本小题满分12分)如图,四棱锥P-ABCD中,PA⊥平面ABCD,PA=AB=BC=2,E为PA的中点,过E作平行于底面的平面EFGH,分别与另外三条侧棱相交于点F、G、H. 已知底面ABCD为直角梯形,AD∥BC,AB⊥AD,∠BCD=135°.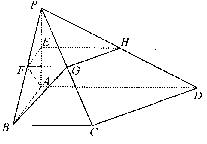
(1)求异面直线AF与BG所成的角的大小;
(2)求平面APB与平面CPD所成的锐二面角的大小.